第86页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
1. 下列几何图形与相应语言描述相符的是(
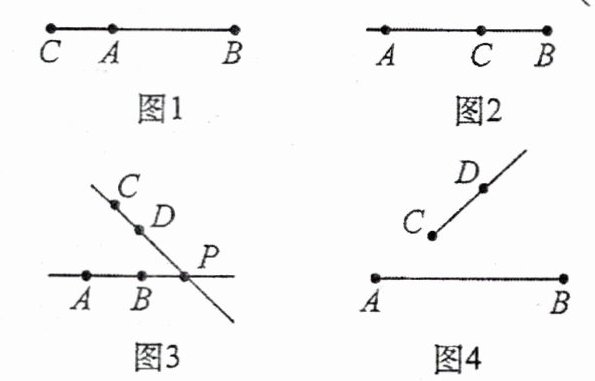
A.如图 1,延长线段 $ AB $ 到点 $ C $
B.如图 2,点 $ B $ 在射线 $ CA $ 上
C.如图 3,直线 $ AB $ 的延长线与直线 $ CD $ 的延长线相交于点 $ P $
D.如图 4,射线 $ CD $ 和线段 $ AB $ 没有交点
D
)
A.如图 1,延长线段 $ AB $ 到点 $ C $
B.如图 2,点 $ B $ 在射线 $ CA $ 上
C.如图 3,直线 $ AB $ 的延长线与直线 $ CD $ 的延长线相交于点 $ P $
D.如图 4,射线 $ CD $ 和线段 $ AB $ 没有交点
答案:
1.D
2. 下列三种实践方式:木匠弹墨线、打靶瞄准、拉绳插秧等,反映了直线的一个基本事实是

两点确定一条直线
.
答案:
2.两点确定一条直线
3. 根据条件画出图形,并解答问题:
(1) 如图,已知四个点 $ A $,$ B $,$ C $,$ D $.
① 连接 $ BC $,画射线 $ AD $.
② 画出一点 $ P $,使点 $ P $ 到 $ A $,$ B $,$ C $,$ D $ 四点的距离之和最小,理由是
(2) 在(1)的条件下填空:图中共有

(1) 如图,已知四个点 $ A $,$ B $,$ C $,$ D $.
① 连接 $ BC $,画射线 $ AD $.
② 画出一点 $ P $,使点 $ P $ 到 $ A $,$ B $,$ C $,$ D $ 四点的距离之和最小,理由是
两点之间线段最短
.(2) 在(1)的条件下填空:图中共有
8
条线段.
答案:
3.解:
(1)①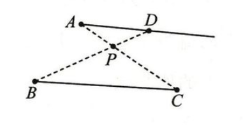
②两点之间线段最短
(2)8
3.解:
(1)①

②两点之间线段最短
(2)8
4. (2024·合肥巢湖市期末) 如图,点 $ B $,$ C $ 在线段 $ AD $ 上,$ AC = BD $,$ BC = 3AB $. 如果 $ CD = \frac{1}{5} $,那么 $ BC $ 的长度为(

A.$ \frac{3}{5} $
B.$ \frac{4}{5} $
C.$ \frac{5}{4} $
D.$ 1 $
A
)
A.$ \frac{3}{5} $
B.$ \frac{4}{5} $
C.$ \frac{5}{4} $
D.$ 1 $
答案:
4.A
5. 在直线 $ l $ 上顺次取 $ A $,$ B $,$ C $ 三点,使得 $ AB = 8 cm $,$ BC = 6 cm $. 如果 $ O $ 是线段 $ AC $ 的中点,那么线段 $ AO $ 的长为
7cm
.
答案:
5.7cm
6. (2024·合肥高新区期末) 如图,$ D $ 是 $ AB $ 的中点,$ E $ 是 $ BC $ 的中点,$ AE = 10 $,$ CD = 8 $,则线段 $ DE $ 的长为

6
.
答案:
6.6
7. 定义:如图,有公共端点 $ B $ 的两条线段 $ BA $,$ BC $ 组成一条折线 $ A - B - C $,若该折线 $ A - B - C $ 上一点 $ O $ 把这条折线分成相等的两部分,我们把这个点 $ O $ 叫作这条折线的“折中点”. 已知点 $ Q $ 是折线 $ M - P - N $ 的“折中点”,且点 $ Q $ 在 $ NP $ 上,$ K $ 为线段 $ MP $ 的中点. 若 $ PQ = 2PK = 4 $,则线段 $ NP $ 的长为
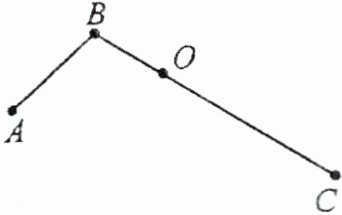
12
.
答案:
7.12
8. (2024·合肥高新区期末) 如图,线段 $ AB = 1 $,$ A_1 $ 是线段 $ AB $ 的中点,$ A_2 $ 是线段 $ A_1B $ 的中点,$ A_3 $ 是线段 $ A_2B $ 的中点……以此类推,$ A_{n + 1} $ 是线段 $ A_nB $ 的中点.
(1) 线段 $ A_3B $ 的长为
(2) 线段 $ A_nB $ 的长为
(3) 求 $ AA_1 + A_1A_2 + A_2A_3 + \cdots + A_6A_7 $ 的值.
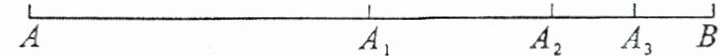
(1) 线段 $ A_3B $ 的长为
\frac{1}{8}
.(2) 线段 $ A_nB $ 的长为
\frac{1}{2^{n}}
.(3) 求 $ AA_1 + A_1A_2 + A_2A_3 + \cdots + A_6A_7 $ 的值.
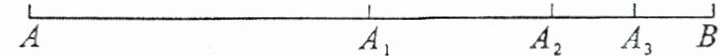
答案:
8.解$:(1)\frac{1}{8} (2)\frac{1}{2^{n}} (3)AA_{1}+A_{1}A_{2}+A_{2}A_{3}+\cdots+A_{6}A_{7}=AB -A_{7}B=1 - \frac{1}{2^{7}}=\frac{127}{128}$
9. (2024·合肥蜀山区期末) 已知一副直角三角板按如图所示的方式放置,其中 $ \angle COD = 60° $,$ \angle AOB = 45° $,经测量 $ \angle BOC = 80° $,则 $ \angle AOD $ 度数为(
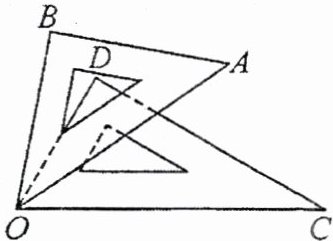
A.$ 20° $
B.$ 25° $
C.$ 35° $
D.$ 45° $
B
)
A.$ 20° $
B.$ 25° $
C.$ 35° $
D.$ 45° $
答案:
9.B
查看更多完整答案,请扫码查看


