《2025年名校课堂七年级数学上册北师大版》

10. 淇淇在计算$(-2)^{3}-(-1)^{2024}+12÷ (\frac{1}{2}-\frac{1}{3})$时，步骤如下。
解：原式$=-6-(-2024)+12÷ \frac{1}{2}-12÷ \frac{1}{3}\cdots\cdots$①
$=-6 + 2024+24-36\cdots\cdots$②
$=2006\cdots\cdots$③
(1) 淇淇的计算过程中开始出现错误的步骤是①。(填序号)
(2) 请给出正确的解题过程。

答案： 10解
(1)①
(2)原式$=-8-1+12÷\frac{1}{6}=-9+72=63$

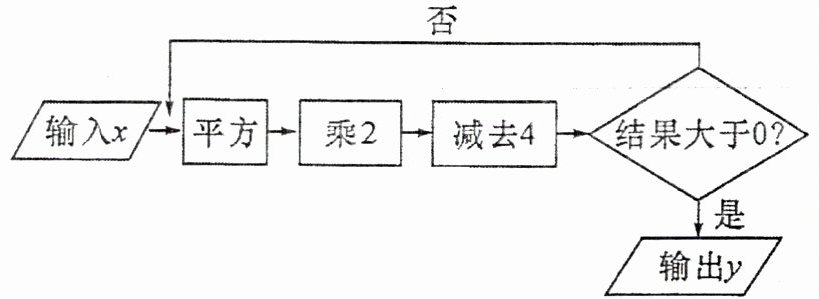
11. 数学课上，老师给同学们编了如图所示的计算程序，当输入$x$的值是$1$时，输出$y$的值是4。

答案： 11.4

12. (2024·甘肃)定义一种新运算$*$，规定运算法则为：$m*n = m^{n}-mn$($m$，$n$均为整数，且$m\neq 0$)。例：$2*3 = 2^{3}-2× 3 = 2$，则$(-2)*2=$8$$。

答案： 12.8

13. 计算：
(1) $2× (-1)^{3}-4÷ (-\frac{1}{2})× 3$。
(2) $[(-1)^{2025}× \vert -\frac{3}{2}\vert +(-0.5)]÷ (-\frac{1}{3})$。

答案： 13解
(1)原式=2×(-1)+4×2×3=-2+24=22
(2)原式$=(-1×\frac{3}{2}-\frac{1}{2})×(-3)=-2×(-3)=6$

14. 近年来，绿色低碳的骑行活动受到年轻人的青睐，一句“青春没有售价，夜骑开封拿下”成功吸引了数万名郑州的大学生夜骑共享单车到开封。共享单车的开关两种状态可以用二进制中的$1$和$0$两个数字表示，约定逢二进一，二进制数$101$转化为十进制数的方法为：从右起，第一位上的$1$表示$1× 2^{0}$，第二位上的$0$表示$0× 2^{1}$，第三位上的$1$表示$1× 2^{2}$，故二进制数$101$转化为十进制数为$1× 2^{0}+0× 2^{1}+1× 2^{2}=5$（规定$2^{0}=1$）。求二进制数$1011001$转化为十进制数是多少。

答案： 14解由题意可得二进制数1011001转化为十进制数是1×2⁶+0×2⁵+1×2⁴+1×2³+0×2²+0×2¹+1×2⁰=1×64+0+1×16+1×8+0+0+1×1=64+0+16+8+0+0+1=89

15. (教材 P65“尝试·交流”变式)“24 点”游戏规则如下：在一副扑克牌(去掉大、小王)中取四张，根据牌面上的数字进行混合运算(每张牌只能用一次)，使得运算结果为$24$或$-24$。其中红色牌代表负数，黑色牌代表正数，$A$，$J$，$Q$，$K$分别代表$1$，$11$，$12$，$13$。例如：黑桃$A$，$2$，$3$和红桃$2$可作如下运算：$2^{3}× (-2 - 1)=-24$或$2^{3}× [1-(-2)] = 24$。
(1) 现在四张牌分别为红桃$2$、黑桃$3$、方块$3$和梅花$6$，运用上述规则写出三种不同运算方法的算式，使其结果为$24$或$-24$。
①-2×(-3-3-6)=24；
②(-2)³×[6+(-3)]=-24；
③[-2+3-(-3)]×6=24。
(2) 若四张牌分别为梅花$A$、黑桃$2$、黑桃$4$和方块$8$，则如何运算使其结果为$24$或$-24$呢？(写出一种即可)

答案： 15解
(1)①-2×(-3-3-6)=24 ②(-2)³×[6+(-3)]=-24 ③[-2+3-(-3)]×6=24(答案不唯一)
(2)答案不唯一，如4²-[1×(-8)]=24