《2025年名校课堂七年级数学上册北师大版》

1. 如果盈利100元记作+100元，那么亏损50元记作－50元.

答案： 1.－50

2. 下列说法：①0是最小的整数；②有理数不是正数就是负数；③正整数、负整数、正分数、负分数统称为有理数；④非负数就是正数；⑤$\frac{22}{7}$是无限不循环小数，所以不是有理数. 其中，错误说法的个数为(D)

A.2
B.3
C.4
D.5

答案： 2.D

3. (2024·宿州埇桥区期中)如图，在数轴上，小手遮挡住的点表示的数可能是(C)


A.-1.5
B.-2.5
C.-0.5
D.0.5

答案： 3.C

4. 下列说法中，正确的是(C)

A.2与-2互为倒数
B.2与$\frac{1}{2}$互为相反数
C.0的相反数是0
D.2的绝对值是-2

答案： 4.C

5. (2024·宿州埇桥区期中)如图，在数轴上点A表示的数a是(-2)³的相反数，点B表示的数b是最小的正整数，点C表示的数c是绝对值是3的负整数. 若将数轴折叠，使得点A与点C重合，则与点B重合的点表示的数是4.

答案： 5.4

考点3 有理数的大小比较

答案： 由于您未提供具体的题目内容，无法进行解答。请您补充具体的题目信息，以便我按照要求为您完成解析和答案。

6. 下列各数：(-1)²，|-2|，0，-(-3)，其中最大的数是(C)

A.(-1)²
B.0
C.-(-3)
D.|-2|

答案： 6.C

7. 大于-4.2且小于3.8的整数有(D)

A.5个
B.6个
C.7个
D.8个

答案： 7.D

8. 在数轴上表示下列各数，并用“＜”连接.
3，-(-2)，-1.5，0，-|-1|，-3$\frac{1}{3}$.

答案：
8.解：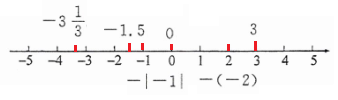
从小到大排列为：$-3\frac{1}{3}＜－1.5＜－$|－1|＜0＜－(－2)＜3。

9. 如果a与b互为相反数，那么下列各式不正确的是(C)

A.a + b = 0
B.|a| = |b|
C.a - b = 0
D.a = -b

答案： 9.C

10. (2024·宿州埇桥区期中)若a与2互为相反数，则|$\frac{1}{2}$a - 1| =(A)

A.2
B.-2
C.0
D.-1

答案： 10.A

11. 有理数a，b在数轴上的位置如图所示，则下列说法不正确的是(B)


A.ab ＜ 0
B.a + b ＞ 0
C.b - a ＞ 0
D.|b| ＜ |a|

答案： 11.B

12. 已知|x| = 5，y = -4，且x ＞ y，则x - y的值为9.

答案： 12.9

13. 若|a - 2|与|b + 4|互为相反数，则a + b的值为－2.

答案： 13.－2

14. 计算：-1²⁰²⁴ - (2 - 0.5)×$\frac{1}{3}$×|1 - (-3)²| =－5.

答案： 14.－5

15. 某同学把5×(□ - 6)错抄为5×□ - 6，若正确的计算结果为m，抄错后的计算结果为n，则m - n =－24.

答案： 15.－24

16. 计算：
(1) (-21) - (-$\frac{6}{5}$) + (-9) - $\frac{1}{2}$.
(2) ($\frac{1}{9}$ - $\frac{2}{7}$ - $\frac{4}{21}$)×(-63).
(3) -2⁴ ÷ (-2)³ - 3² × | - $\frac{1}{3}$ | + (-1)²⁰²⁵.

答案： 16.解：
(1)原式=(－21－9)+(1.2－0.5)=－30+0.7=－29.3。
(2)原式$=\frac{1}{9}×(－63)－\frac{2}{7}×(－63)－\frac{4}{21}×(－63)=－7+18+12=23。$
(3)原式$=－16÷(－8)－9×\frac{1}{3}－1=2－3－1=－2。$