《2025年世纪金榜金榜学案九年级物理全一册人教版》

3.(跨学科·物理与社会生活)如图是小明家用的天然气热水器,小明为了估测该热水器的热效率,他进行了如下操作:
①把家里自动洗衣机的“水量”设置为30L；
②将热水器的出水温度设定为$42^{\circ }C$；
③记下天然气热水器上显示的自来水温度为$28^{\circ }C$；
④将热水器输出的热水注入洗衣机,当注入水的体积达到30L时洗衣机便会自动停止注水,用手表测出了注水时间为7min30s；
⑤小明检查燃气表,发现热水器正常工作一分钟,消耗天然气$0.01m^{3}$,天然气的热值是$3.2×10^{7}J/m^{3}$。
请你根据以上信息,解答下列问题:

(1)7min30s内,天然气完全燃烧放出的热量是多少?
(2)由测量并计算可知,该热水器烧水的热效率为多少。

答案： 3.解:
(1)7 min 30 s内消耗的天然气体
积:$V_{气}=7.5×0.01m^{3}=0.075m^{3}$,天
然气燃烧放出的热量为:
$Q_{放}=V_{气}q=0.075m^{3}×3.2×10^{7}J/m^{3}$
$=2.4×10^{6}J;$
(2)被热水器加热的水的体积为:
$V_{水}=30L=30dm^{3}=0.03m^{3};$
根据$ρ=\frac {m}{V}$可得水的质量:
$m=ρV_{水}=1×10^{3}kg/m^{3}×0.03m^{3}$
$=30kg;$
水吸收的热量:
$Q_{吸}=cmΔt=4.2×10^{3}J/(kg\cdot ^{\circ }C)×$
$30kg×(42^{\circ }C-28^{\circ }C)=1.764×10^{6}J;$
热水器烧水的效率:
$η=\frac {Q_{吸}}{Q_{放}}=\frac {1.764×10^{6}J}{2.4×10^{6}J}=73.5\% $。

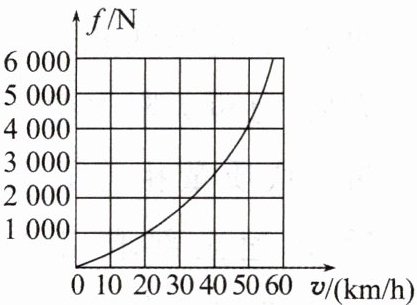
4.(2024秋·常州期中)某新型混合动力汽车有多种提供动力的方式。内燃机不工作时,蓄电池向车轮输送能量;内燃机启动时,既可以向车轮输送能量,又可以给蓄电池充电。如图所示为车速与所受阻力的关系图像。在某次测试中只由内燃机提供能量,汽车以50km/h的速度在水平面上匀速行驶了0.5h,测试过程中共消耗8kg燃料(假设燃料完全燃烧),同时蓄电池的电能增加了$5.12×10^{7}J$,假设所用燃料的热值为$4.5×10^{7}J/kg$。求:

(1)测试过程中燃料燃烧产生的热量；
(2)测试过程中汽车牵引力做的功；
(3)内燃机的效率。

答案： 4.解:
(1)燃料完全燃烧放出的热量为:
$Q_{放}=mq_{燃料}=8kg×4.5×10^{7}J/kg$
$=3.6×10^{8}J;$
(2)汽车以50 km/h的速度匀速行驶了
0.5h,则汽车行驶的路程为:$s=vt=$
$50km/h×0.5h=25km=25000m,$
由图像可知,当汽车速度达到50 km/h
时,汽车受到的阻力是$f=4000N$,因
为汽车做匀速直线运动,处于平衡状
态,牵引力和阻力是一对平衡力,所以
牵引力$F=f=4000N$,测试过程中汽
车牵引力做的功为:
$W=Fs=4000N×25000m=1×10^{8}J;$
(3)蓄电池增加的电能为$E=5.12×10^{7}J,$
有效利用的能量等于汽车牵引力做的
功与转化成电能的能量之和,即
$W_{有}=W+E=1×10^{8}J+5.12×10^{7}J=$
$1.512×10^{8}J,$
在该次测试中内燃机的效率:
$η=\frac {W_{有}}{Q_{放}}=\frac {1.512×10^{8}J}{3.6×10^{8}J}=42\% $。