《2025年世纪金榜金榜学案九年级物理全一册人教版》

1.(2025·阜阳质检)如图是一种新型的金属冰块,与普通冰块相比,金属冰块使用起来更加方便,且可无限次循环使用,既经济又耐用,现将三块质量相等的金属冰块冷冻至$-20^{\circ }C$后,迅速全部取出放入另一个装有初温为$30^{\circ }C$的水杯中,放入全部金属冰块后水温最终下降到$20^{\circ }C$。已知每块金属冰块的质量为100g,杯中水的质量为200g,该过程不计热量损失,$c_{水}= 4.2×10^{3}J/(kg\cdot ^{\circ }C)$。求:
(1)三块金属冰块吸收的热量是多少。
(2)该金属冰块的比热容是多少。

答案： 1.解:
(1)水放出的热量:
$Q_{放}=c_{水}m_{水}(t_{0水}-t_{水})$
$=4.2×10^{3}J/(kg\cdot ^{\circ }C)×0.2kg×$
$(30^{\circ }C-20^{\circ }C)=8.4×10^{3}J;$
不计热量损失,则金属冰块吸收的热量
为$Q_{吸}=Q_{放}=8.4×10^{3}J;$
(2)放入全部金属冰块后水温最终下降
到$20^{\circ }C$,故金属冰块此时的温度为
$t_{金}=20^{\circ }C$。
由$Q_{吸}=c_{金}m_{金}(t_{金}-t_{0金})$得该金属冰块
的比热容:
$c_{金}=\frac {Q_{吸}}{m_{金}(t_{金}-t_{0金})}=$
$\frac {8.4×10^{3}J}{3×0.1kg×[20^{\circ }C-(-20^{\circ }C)]}$
$=0.7×10^{3}J/(kg\cdot ^{\circ }C)$。

2.(2024秋·苏州质检)如图甲,网上曾热销一种“55度杯”,称“能很快将开水变成适饮的温水,而后又能将凉水变成适饮的温水”。为破解此中秘密,某中学物理小组设计了如图乙模型。设此杯内胆中被封存着300g水,室温$20^{\circ }C$;现向杯中倒入200g、$100^{\circ }C$开水,忽略内胆及空间的热能消耗,热平衡后,求:

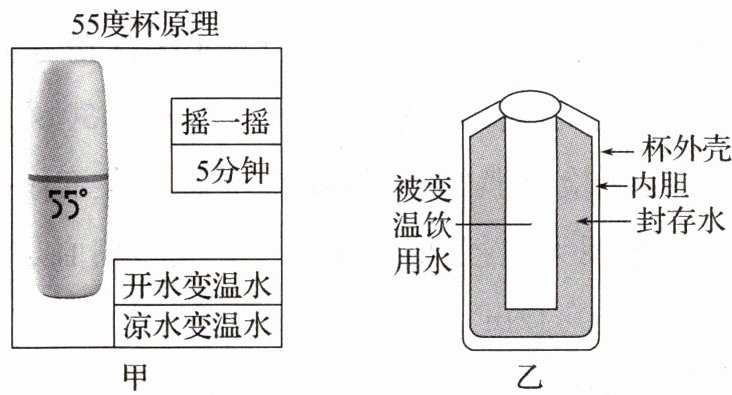
(1)杯内水温为多少?
(2)饮用后迅速将200g室温矿泉水倒入该杯,摇一摇,矿泉水的温度将上升至多少?

答案： 2.解:
(1)热水放出的热量:
$Q_{放}=cm(t_{0}-t_{1})$,冷水吸收的热量:
$Q_{吸}=cm(t_{1}-t_{0}')$;假设热水放出的热量
全部被冷水吸收,所以$Q_{吸}=Q_{放}$,即
$4.2×10^{3}J/(kg\cdot ^{\circ }C)×0.2kg×$
$(100^{\circ }C-t_{1})=4.2×10^{3}J/(kg\cdot ^{\circ }C)×$
$0.3kg×(t_{1}-20^{\circ }C);$
解得$t_{1}=52^{\circ }C$。
(2)迅速将200g室温矿泉水倒入该杯,
摇一摇,矿泉水的温度可升至$t_{2}$,即
$4.2×10^{3}J/(kg\cdot ^{\circ }C)×0.3kg×(52^{\circ }C$
$-t_{2})=4.2×10^{3}J/(kg\cdot ^{\circ }C)×0.2kg$
$×(t_{2}-20^{\circ }C);$
解得$t_{2}=39.2^{\circ }C$。