《2025年暑假乐园现代教育出版社八年级数学人教版》

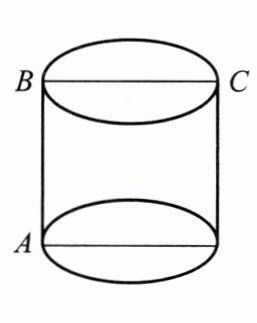
1. 右图所示圆柱的高AB=3，底面直径BC=3。现在有一只蚂蚁想从A处沿圆柱表面爬到对角C处捕食，试求出蚂蚁爬行的最短距离。

$\frac{3}{2}\sqrt{4 + \pi^{2}}$

答案： 【解析】：将圆柱的侧面展开得到一个长方形，长方形的长为底面圆的周长的一半，底面圆的直径$BC = 3$，根据圆的周长公式$C=\pi d$（$d$为直径），则底面圆周长的一半为$\frac{1}{2}\times\pi\times3=\frac{3\pi}{2}$，长方形的宽$AB = 3$。蚂蚁从$A$处沿圆柱表面爬到对角$C$处的最短距离就是这个长方形的对角线长度。根据勾股定理$a^2 + b^2 = c^2$（其中$a$、$b$为直角边，$c$为斜边），这里$a = 3$，$b=\frac{3\pi}{2}$，所以$AC=\sqrt{3^{2}+(\frac{3\pi}{2})^{2}}=\sqrt{9 + \frac{9\pi^{2}}{4}}=\frac{3}{2}\sqrt{4 + \pi^{2}}$。
【答案】：$\frac{3}{2}\sqrt{4 + \pi^{2}}$

2. 周末，明明和爸爸一起去钓鱼。已知钓鱼竿AC的长为6m，露在水面上的鱼线BC的长为3$\sqrt{2}$m（如图所示）。明明想看看鱼钩上的情况，爸爸把鱼竿AC转动到AC'的位置，此时露在水面上的鱼线B'C'的长为$\sqrt{34}$m。爸爸请明明帮他算算BB'的长。如果你是明明，该怎么算呢？

BB'的长为$2\sqrt{2}m$或$4\sqrt{2}m$。

答案： 【解析】：
首先，根据勾股定理，在$Rt\triangle ABC$中，$AB=\sqrt{AC^{2}-BC^{2}}$。
已知$AC = 6m$，$BC = 3\sqrt{2}m$，则$AB=\sqrt{6^{2}-(3\sqrt{2})^{2}}=\sqrt{36 - 18}=\sqrt{18}=3\sqrt{2}(m)$。
然后，在$Rt\triangle AB'C'$中，$AB'=\sqrt{AC'^{2}-B'C'^{2}}$。
因为$AC' = AC = 6m$，$B'C'=\sqrt{34}m$，所以$AB'=\sqrt{6^{2}-(\sqrt{34})^{2}}=\sqrt{36 - 34}=\sqrt{2}(m)$。
最后，分两种情况讨论$BB'$的长度：
情况一：当$B'$在$AB$的延长线上时，$BB'=AB + AB'=3\sqrt{2}+\sqrt{2}=4\sqrt{2}(m)$。
情况二：当$B'$在$AB$上时，$BB'=AB - AB'=3\sqrt{2}-\sqrt{2}=2\sqrt{2}(m)$。
【答案】：$2\sqrt{2}m$或$4\sqrt{2}m$