《2025年暑假乐园现代教育出版社八年级数学人教版》

学习了二次根式以后，你知道海伦公式与秦九韶公式吗?下面我们一起去了解一下吧!
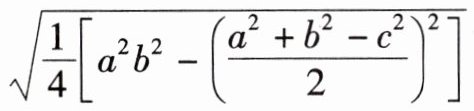
我们知道，如果一个三角形的三边长固定，那么这个三角形就固定.若给出任意一个三角形的三边长，你能求出它的面积吗?翻阅了各种资料后可知，古希腊的几何学家海伦(Heron)在数学史上以解决几何测量问题而闻名，在他的著作《量度论》中，给出了一个公式：如果一个三角形的三边长分别为a，b，c，那么记三角形的面积为$S=\sqrt {p(p-a)(p-b)(p-c)}$，其中$p=\frac {a+b+c}{2}$.这一公式后来被称为海伦公式.
其实在我国古代算学专著《九章算术》中，已经有求三角形面积的公式——“底乘高的一半”.但在实际丈量三角形土地面积时，要找出高来并非易事，所以古人想到了三角形的三条边，这样求三角形的面积就方便多了.但是怎样根据三边的长度来求三角形的面积呢?直到南宋，中国著名的数学家秦九韶提出了“三斜求积术”.他把三角形的三条边分别称为小斜、中斜和大斜，“术”即方法，化为公式如下：$S=\sqrt {\frac {1}{4}[a^{2}b^{2}-(\frac {a^{2}+b^{2}-c^{2}}{2})^{2}]}$(a，b，c分别为小斜、中斜、大斜).
秦九韶公式与海伦公式等价.对比这两个公式，我们发现海伦公式形式美观，便于记忆；但是如果一个三角形的三边长是无理数的时候，还是用秦九韶公式处理比较方便.聪明的你能够从秦九韶公式推导出海伦公式来吗?
能从秦九韶公式推导出海伦公式，推导过程如下：
$\begin{aligned}S&=\sqrt{\frac{1}{4}[a^{2}b^{2}-(\frac{a^{2}+b^{2}-c^{2}}{2})^{2}]}\\&=\sqrt{\frac{1}{4}(ab+\frac{a^{2}+b^{2}-c^{2}}{2})(ab-\frac{a^{2}+b^{2}-c^{2}}{2})}\\&=\sqrt{\frac{1}{16}(2ab+a^{2}+b^{2}-c^{2})(2ab - a^{2}-b^{2}+c^{2})}\\&=\sqrt{\frac{1}{16}[(a + b)^{2}-c^{2}][c^{2}-(a - b)^{2}]}\\&=\sqrt{\frac{1}{16}(a + b + c)(a + b - c)(c + a - b)(c - a + b)}\\\end{aligned}$
因为$p=\frac{a + b + c}{2}$，所以$a + b + c = 2p$，$a + b - c = 2p - 2c$，$c + a - b = 2p - 2b$，$c - a + b = 2p - 2a$。
$\begin{aligned}S&=\sqrt{\frac{1}{16}×2p×(2p - 2c)×(2p - 2b)×(2p - 2a)}\\&=\sqrt{p(p - a)(p - b)(p - c)}\end{aligned}$

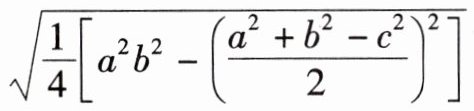
答案： 【解析】：
$\begin{aligned}S&=\sqrt{\frac{1}{4}[a^{2}b^{2}-(\frac{a^{2}+b^{2}-c^{2}}{2})^{2}]}\\&=\sqrt{\frac{1}{4}(ab+\frac{a^{2}+b^{2}-c^{2}}{2})(ab-\frac{a^{2}+b^{2}-c^{2}}{2})}\\&=\sqrt{\frac{1}{16}(2ab+a^{2}+b^{2}-c^{2})(2ab - a^{2}-b^{2}+c^{2})}\\&=\sqrt{\frac{1}{16}[(a + b)^{2}-c^{2}][c^{2}-(a - b)^{2}]}\\&=\sqrt{\frac{1}{16}(a + b + c)(a + b - c)(c + a - b)(c - a + b)}\\\end{aligned}$
因为$p=\frac{a + b + c}{2}$，所以$a + b + c = 2p$，$a + b - c = 2p - 2c$，$c + a - b = 2p - 2b$，$c - a + b = 2p - 2a$。
$\begin{aligned}S&=\sqrt{\frac{1}{16}\times2p\times(2p - 2c)\times(2p - 2b)\times(2p - 2a)}\\&=\sqrt{p(p - a)(p - b)(p - c)}\end{aligned}$
【答案】：能从秦九韶公式推导出海伦公式，推导过程如上述解析。