2025年单元双测全优测评卷七年级数学下册沪科版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年单元双测全优测评卷七年级数学下册沪科版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第71页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
21. 如图,在三角形ABC中,点D,E分别在AB,BC上,且DE//AC,∠1 = ∠2.
(1)求证:AF//BC;
(2)若AC平分∠BAF,∠B = 36°,求∠1的度数.
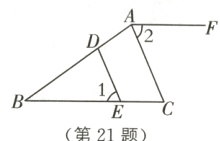
(1)求证:AF//BC;
(2)若AC平分∠BAF,∠B = 36°,求∠1的度数.

答案:
(1)
∵DE//AC,
∴∠1 = ∠C.
∵∠1 = ∠2,
∴∠C = ∠2,
∴AF//BC.
(2)
∵AF//BC,
∴∠B + ∠BAF = 180°.
∵∠B = 36°,
∴∠BAF = 144°.
∵AC平分∠BAF,
∴∠2 = $\frac{1}{2}$∠BAF = 72°.
∵∠1 = ∠2,
∴∠1 = 72°.
方法诠释 本题考查了平行线的性质和判定的综合应用. 要证明两直线平行,就要利用平行线的判定定理,找出两直线被第三条直线所截的同位角、内错角或同旁内角的关系. 题中有内错角与第三个角的关系,利用平行线的性质和中间量就可以证明内错角相等.
(1)
∵DE//AC,
∴∠1 = ∠C.
∵∠1 = ∠2,
∴∠C = ∠2,
∴AF//BC.
(2)
∵AF//BC,
∴∠B + ∠BAF = 180°.
∵∠B = 36°,
∴∠BAF = 144°.
∵AC平分∠BAF,
∴∠2 = $\frac{1}{2}$∠BAF = 72°.
∵∠1 = ∠2,
∴∠1 = 72°.
方法诠释 本题考查了平行线的性质和判定的综合应用. 要证明两直线平行,就要利用平行线的判定定理,找出两直线被第三条直线所截的同位角、内错角或同旁内角的关系. 题中有内错角与第三个角的关系,利用平行线的性质和中间量就可以证明内错角相等.
七、(本题满分12分)
22. 如图,AB//CD,MG平分∠EMA,NH平分∠MNC.
(1)MG//NH吗?为什么?
(2)如果把条件“MG平分∠EMA”改为“MG平分∠BMN”,MG//NH还成立吗?请说明理由.

22. 如图,AB//CD,MG平分∠EMA,NH平分∠MNC.
(1)MG//NH吗?为什么?
(2)如果把条件“MG平分∠EMA”改为“MG平分∠BMN”,MG//NH还成立吗?请说明理由.

答案:
(1)平行. 理由如下:
∵AB//CD,
∴∠EMA = ∠MNC.
∵MG平分∠EMA,NH平分∠MNC,
∴∠EMG = $\frac{1}{2}$∠EMA,∠MNH = $\frac{1}{2}$∠MNC,
∴∠EMG = ∠MNH,
∴MG//NH.
(2)成立. 理由如下:
∵AB//CD,
∴∠BMN = ∠CNM.
∵MG平分∠BMN,NH平分∠MNC,
∴∠GMN = $\frac{1}{2}$∠BMN,∠HNM = $\frac{1}{2}$∠CNM,
∴∠HNM = ∠GMN,
∴MG//NH.
(1)平行. 理由如下:
∵AB//CD,
∴∠EMA = ∠MNC.
∵MG平分∠EMA,NH平分∠MNC,
∴∠EMG = $\frac{1}{2}$∠EMA,∠MNH = $\frac{1}{2}$∠MNC,
∴∠EMG = ∠MNH,
∴MG//NH.
(2)成立. 理由如下:
∵AB//CD,
∴∠BMN = ∠CNM.
∵MG平分∠BMN,NH平分∠MNC,
∴∠GMN = $\frac{1}{2}$∠BMN,∠HNM = $\frac{1}{2}$∠CNM,
∴∠HNM = ∠GMN,
∴MG//NH.
查看更多完整答案,请扫码查看


