2025年单元双测全优测评卷七年级数学下册沪科版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年单元双测全优测评卷七年级数学下册沪科版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第5页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
21. 甲、乙、丙三人组成学习小组在数学练习课上互相讨论. 甲写了一个数9,乙写了一个数16,他们要求丙再写一个数,使这三个数中的一个数是另外两个数乘积的平方根,那么丙能写出符合条件的数吗?若能写出,能写几个?若不能写出,请说明理由.
答案:
设丙写出的符合条件的数为$x$.①$x^{2}=9\times16$,$\therefore x=\pm12$;②$16x = 9^{2}$,$\therefore x=\frac{81}{16}$;③$9x = 16^{2}$,$\therefore x=\frac{256}{9}$.综上所述,丙能写出的符合条件的数有4个,分别为$\pm12$,$\frac{81}{16}$,$\frac{256}{9}$.
22. 某金属冶炼厂将27个大小相同的正方体钢铁在炉火中熔化,铸成一个长方体钢铁,此长方体的长、宽、高分别为160 cm,80 cm和40 cm,求原来每个正方体钢铁的棱长.
答案:
由题意,得$\sqrt[3]{\frac{160\times80\times40}{27}}=\sqrt[3]{\frac{512000}{27}}=\frac{80}{3}(\text{cm})$.故原来每个正方体钢铁的棱长为$\frac{80}{3}\text{cm}$.
23. 中考新考法 数形结合 折叠纸面,若在数轴上−1表示的点与5表示的点重合,回答以下问题:
(1)数轴上10表示的点与_______表示的点重合;
(2)若数轴上M,N两点之间的距离为2024(M在N的左侧),且M,N两点经折叠后重合,求M,N两点表示的数;
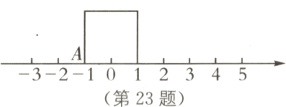
(3)如图,边长为2的正方形有一顶点A落在数轴上表示−1的点处,将正方形在数轴上向右滚动(无滑动),正方形的一边与数轴重合记为滚动一次,则正方形滚动2024次后,与数轴上表示点A的数折叠后重合的数为_______.
(1)数轴上10表示的点与_______表示的点重合;
(2)若数轴上M,N两点之间的距离为2024(M在N的左侧),且M,N两点经折叠后重合,求M,N两点表示的数;
(3)如图,边长为2的正方形有一顶点A落在数轴上表示−1的点处,将正方形在数轴上向右滚动(无滑动),正方形的一边与数轴重合记为滚动一次,则正方形滚动2024次后,与数轴上表示点A的数折叠后重合的数为_______.

答案:
(1)$-6$
(2)由题意,得$M$,$N$两点在数轴上关于2所表示的点对称.$\because$数轴上$M$,$N$两点之间的距离为2024,$\therefore\frac{1}{2}MN=\frac{1}{2}\times2024 = 1012$,$\therefore 2 + 1012 = 1014$,$2-1012=-1010$,$\therefore$点$M$表示的数为$-1010$,点$N$表示的数为1014.
(3)$-4043$ [解析]$\because$边长为2的正方形有一顶点$A$落在数轴上表示$-1$的点处,$\therefore$正方形滚动第3次、第4次时,点$A$落在数轴上表示7的点处,$7=-1 + 8\times1$;正方形滚动第7次、第8次时,点$A$落在数轴上表示15的点处,$15=-1 + 8\times2$;正方形滚动第11次、第12次时,点$A$落在数轴上表示23的点处,$23=-1 + 8\times3$;$\cdots$,$\therefore$正方形滚动第$(4n - 1)$($n$是正整数)次、第$4n$次时,点$A$落在数轴上表示$(-1 + 8n)$的点处.$\because 2024 = 4\times506$,$\therefore$正方形滚动2024次后,数轴上表示点$A$的数为$-1 + 8\times506 = 4047$.此时,点$A$距离数轴上2表示的点的距离为$4047-2 = 4045$,而$2-4045=-4043$,$\therefore$正方形滚动2024次后,数轴上表示点$A$的数与折叠后的数$-4043$重合.
(1)$-6$
(2)由题意,得$M$,$N$两点在数轴上关于2所表示的点对称.$\because$数轴上$M$,$N$两点之间的距离为2024,$\therefore\frac{1}{2}MN=\frac{1}{2}\times2024 = 1012$,$\therefore 2 + 1012 = 1014$,$2-1012=-1010$,$\therefore$点$M$表示的数为$-1010$,点$N$表示的数为1014.
(3)$-4043$ [解析]$\because$边长为2的正方形有一顶点$A$落在数轴上表示$-1$的点处,$\therefore$正方形滚动第3次、第4次时,点$A$落在数轴上表示7的点处,$7=-1 + 8\times1$;正方形滚动第7次、第8次时,点$A$落在数轴上表示15的点处,$15=-1 + 8\times2$;正方形滚动第11次、第12次时,点$A$落在数轴上表示23的点处,$23=-1 + 8\times3$;$\cdots$,$\therefore$正方形滚动第$(4n - 1)$($n$是正整数)次、第$4n$次时,点$A$落在数轴上表示$(-1 + 8n)$的点处.$\because 2024 = 4\times506$,$\therefore$正方形滚动2024次后,数轴上表示点$A$的数为$-1 + 8\times506 = 4047$.此时,点$A$距离数轴上2表示的点的距离为$4047-2 = 4045$,而$2-4045=-4043$,$\therefore$正方形滚动2024次后,数轴上表示点$A$的数与折叠后的数$-4043$重合.
查看更多完整答案,请扫码查看


