第84页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
1. (2024·新乡原阳县期中)$2\cos 60^{\circ}$的值是(
A.$\frac{1}{2}$
B.$\sqrt{3}$
C.$\sqrt{2}$
D.$1$
D
)A.$\frac{1}{2}$
B.$\sqrt{3}$
C.$\sqrt{2}$
D.$1$
答案:
D
2. 如图,以点$O$为圆心,任意长为半径画弧,与射线$OA$交于点$B$,再以点$B$为圆心,$BO$的长为半径画弧,两弧交于点$C$,画射线$OC$,则$\sin \angle AOC$的值为(
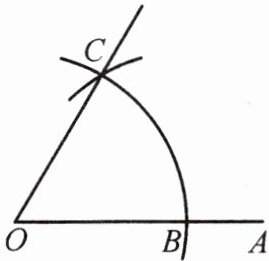
A.$\frac{1}{2}$
B.$\frac{\sqrt{3}}{3}$
C.$\frac{\sqrt{3}}{2}$
D.$\sqrt{3}$
]
C
)
A.$\frac{1}{2}$
B.$\frac{\sqrt{3}}{3}$
C.$\frac{\sqrt{3}}{2}$
D.$\sqrt{3}$
]
答案:
C
$3. $计算:
$(1) (-2)^{2}-2\sin 30^{\circ}=$
$(2) \sin 30^{\circ}+\cos 45^{\circ}=$
$(3) \cos 30^{\circ}\tan 30^{\circ}-\tan 45^{\circ}=$
$(4) \sqrt{2}\sin ^{2}45^{\circ}+2\sin 30^{\circ}=$
$(1) (-2)^{2}-2\sin 30^{\circ}=$
$3$
; $(2) \sin 30^{\circ}+\cos 45^{\circ}=$
$\frac{1 + \sqrt{2}}{2}$
; $(3) \cos 30^{\circ}\tan 30^{\circ}-\tan 45^{\circ}=$
$- \frac{1}{2}$
; $(4) \sqrt{2}\sin ^{2}45^{\circ}+2\sin 30^{\circ}=$
$\frac{\sqrt{2} + 2}{2}$
。
答案:
(1)3;$(2)\frac{1 + \sqrt{2}}{2};$$(3)- \frac{1}{2};$$(4)\frac{\sqrt{2} + 2}{2}$
(1)3;$(2)\frac{1 + \sqrt{2}}{2};$$(3)- \frac{1}{2};$$(4)\frac{\sqrt{2} + 2}{2}$
4. 计算:
(1) $2\cos ^{2}30^{\circ}-2\sin 60^{\circ}\cos 45^{\circ}$;
(2) $\frac{\cos 30^{\circ}}{\tan 60^{\circ}-\sin 60^{\circ}}-\tan 45^{\circ}$。
(1) $2\cos ^{2}30^{\circ}-2\sin 60^{\circ}\cos 45^{\circ}$;
(2) $\frac{\cos 30^{\circ}}{\tan 60^{\circ}-\sin 60^{\circ}}-\tan 45^{\circ}$。
答案:
解:
(1)原式$=2 × (\frac{\sqrt{3}}{2})^2 - 2 × \frac{\sqrt{3}}{2} × \frac{\sqrt{2}}{2} = \frac{3 - \sqrt{6}}{2}. (2)$原式=
$\frac{\frac{\sqrt{3}}{2}}{\sqrt{3} - \frac{\sqrt{3}}{2} - 1} = 0.$
(1)原式$=2 × (\frac{\sqrt{3}}{2})^2 - 2 × \frac{\sqrt{3}}{2} × \frac{\sqrt{2}}{2} = \frac{3 - \sqrt{6}}{2}. (2)$原式=
$\frac{\frac{\sqrt{3}}{2}}{\sqrt{3} - \frac{\sqrt{3}}{2} - 1} = 0.$
5. 在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$\sin A=\frac{\sqrt{3}}{2}$,则$\angle A$的度数是(
A.$30^{\circ}$
B.$45^{\circ}$
C.$60^{\circ}$
D.$90^{\circ}$
C
)A.$30^{\circ}$
B.$45^{\circ}$
C.$60^{\circ}$
D.$90^{\circ}$
答案:
C
6. 若关于$x$的一元二次方程$x^{2}-\sqrt{2}x+\sin \alpha = 0$有两个相等的实数根,则锐角$\alpha =$(
A.$15^{\circ}$
B.$30^{\circ}$
C.$45^{\circ}$
D.$60^{\circ}$
B
)A.$15^{\circ}$
B.$30^{\circ}$
C.$45^{\circ}$
D.$60^{\circ}$
答案:
B
7. 在$\triangle ABC$中,若$\cos A=\frac{\sqrt{2}}{2}$,$\tan B=\sqrt{3}$,则这个三角形一定是(
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰三角形
A
)A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰三角形
答案:
A
8. 在$\triangle ABC$中,若$\vert \sin A-\frac{\sqrt{2}}{2}\vert +(\frac{\sqrt{3}}{2}-\cos B)^{2}=0$,$\angle A$,$\angle B$都是锐角,求$\angle C$的度数。
答案:
解:$\because $|$\sin A - \frac{\sqrt{2}}{2}$|$ + (\frac{\sqrt{3}}{2} - \cos B)^2 = 0, $|$\sin A - \frac{\sqrt{2}}{2}$|与$(\frac{\sqrt{3}}{2} - \cos B)^2$的值均为非负数,$\therefore $|$\sin A - \frac{\sqrt{2}}{2}$|$ = 0, (\frac{\sqrt{3}}{2} - \cos B)^2 = 0,$即
$\sin A = \frac{\sqrt{2}}{2}, \cos B = \frac{\sqrt{3}}{2}. \because \angle A, \angle B$都是锐角,$\therefore \angle A = 45^{\circ}, \angle B =$
$30^{\circ}. \therefore \angle C = 180^{\circ} - 45^{\circ} - 30^{\circ} = 105^{\circ}.$
$\sin A = \frac{\sqrt{2}}{2}, \cos B = \frac{\sqrt{3}}{2}. \because \angle A, \angle B$都是锐角,$\therefore \angle A = 45^{\circ}, \angle B =$
$30^{\circ}. \therefore \angle C = 180^{\circ} - 45^{\circ} - 30^{\circ} = 105^{\circ}.$
9. 求$\tan 30^{\circ}36'$,用计算器的按键顺序正确的是(
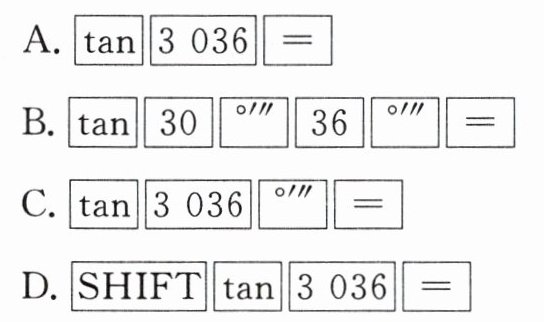
B
)
答案:
B
10. 已知$\sin A = 0.1736$,则锐角$\angle A$的度数大约为(
A.$8^{\circ}$
B.$9^{\circ}$
C.$10^{\circ}$
D.$11^{\circ}$
C
)A.$8^{\circ}$
B.$9^{\circ}$
C.$10^{\circ}$
D.$11^{\circ}$
答案:
C
查看更多完整答案,请扫码查看


