《2025年名校课堂九年级数学上册华师大版8河南专版》

10. (2024·连云港)下列网格中各个小正方形的边长均为 1，阴影部分图形分别记作甲、乙、丙、丁，则其中是相似形的为(D)


A.甲和乙
B.乙和丁
C.甲和丙
D.甲和丁

答案： D

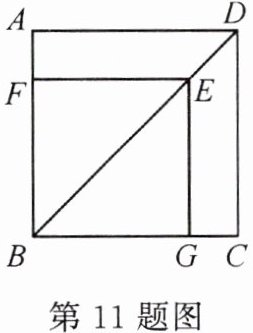
11. 如图，正方形 ABCD 中，点 E 是对角线 BD 上的一点，$ BE = BC $，过点 E 作 $ EF \perp AB $，$ EG \perp BC $，垂足分别为 F，G，则正方形 FBGE 与正方形 ABCD 的边长之比为$\frac{\sqrt{2}}{2}$.

答案： $\frac{\sqrt{2}}{2}$

12. (2024·南阳名校期中联考)如图，四边形 ABCD 是一张矩形纸片. 将其按如图所示的方式折叠：使边 DA 落在边 DC 上，点 A 落在点 H 处，折痕为 DE；使边 CB 落在边 CD 上，点 B 落在点 G 处，折痕为 CF. 若矩形 HEFG 与原矩形 ABCD 相似，$ AD = 1 $，则 CD 的长为$\sqrt{2} + 1$.

答案： $\sqrt{2} + 1$

13. (教材 P60 习题 T2 变式)如图，矩形 ABCD 的长 $ AB = 30 $，宽 $ BC = 20 $.
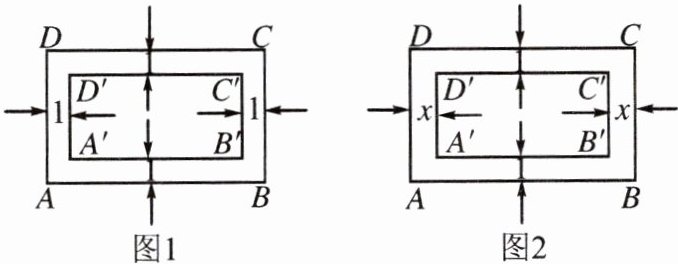
(1) 如图 1，若沿矩形 ABCD 四周有宽为 1 的环形区域，图中所形成的两个矩形 ABCD 与 $ A'B'C'D' $ 相似吗？请说明理由；
(2) 如图 2，当 $ x $ 为多少时，图中的两个矩形 ABCD 与 $ A'B'C'D' $ 相似？

答案： 解：
(1)不相似. 理由：$\because AB = 30$，$A'B' = 28$，$BC = 20$，$B'C' = 18$，而$\frac{28}{30} \neq \frac{18}{20}$，$\therefore$矩形$ABCD$与$A'B'C'D'$不相似.
(2)$\because$矩形$ABCD$与$A'B'C'D'$相似，$\therefore \frac{A'B'}{AB}=\frac{B'C'}{BC}$或$\frac{A'B'}{BC}=\frac{B'C'}{AB}$，$\therefore \frac{30 - 2x}{30}=\frac{20 - 2}{20}$或$\frac{30 - 2x}{20}=\frac{20 - 2}{30}$. 解得$x = 1.5$或$9.\therefore$当$x = 1.5$或$9$时，矩形$ABCD$与$A'B'C'D'$相似.

14. 如图，正方形 ABCD 的边长为 6 cm，E，F 分别是 AB，CD 的三等分点（$ AE ＜ BE $），连结 EF，$ EF // AD $，点 G，H 分别从点 A 和点 E 同时出发，均以 1 cm/s 的速度沿 AD 和 EF 向点 D 和点 F 运动. 当矩形 AGHE 与矩形 DGH F 相似时，求点 G 运动的时间.

答案： 解：$\because$四边形$ABCD$为正方形，$\therefore AD = AB = CD = 6\ cm$. 由题意易得四边形$AEFD$为矩形，$\therefore AD = EF = 6\ cm$，$AE = DF.\because E$，$F$分别是$AB$，$CD$的三等分点($AE ＜ BE$)，$\therefore AE = DF = 2\ cm$. 设点$G$运动$t\ s$时，矩形$AGHE$与矩形$DGHF$相似. 此时$AG = EH = t\ cm$，$DG = HF = (6 - t)\ cm.\therefore \frac{AG}{AE}=\frac{DG}{DF}$或$\frac{AG}{AE}=\frac{DF}{DG}$，$\therefore \frac{t}{2}=\frac{6 - t}{2}$或$\frac{t}{2}=\frac{2}{6 - t}$，解得$t = 3$或$t = 3 \pm \sqrt{5}$. 答：点$G$运动的时间为$3\ s$或$(3 + \sqrt{5})\ s$或$(3 - \sqrt{5})\ s$.