《2025年名校课堂九年级数学上册华师大版8河南专版》

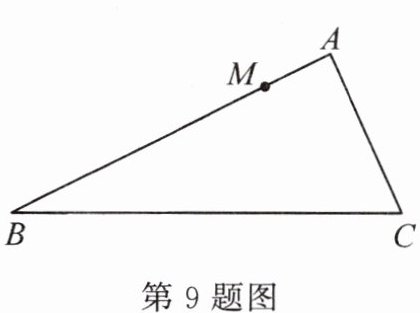
9. (2023·南阳内乡县期中)如图，在$\triangle ABC$中，$AB = 10$，$AC = 5$，点$M$在边$AB$上，且$AM = 2$，点$N$在边$AC$上.当$AN =$1或4时，$\triangle AMN$与原三角形相似.

答案： 9.1或4

10. 如图，在等边三角形$ABC$中，点$D$，$E$分别在$AC$，$AB$上，且$AD:AC = 1:3$，$AE = BE$，则有(B)

A.$\triangle AED\backsim\triangle BED$
B.$\triangle AED\backsim\triangle CBD$
C.$\triangle AED\backsim\triangle ABD$
D.$\triangle BAD\backsim\triangle BCD$

答案： 10.B

11. 在三角形纸片$ABC$中，$AB = 8$，$BC = 4$，$AC = 6$，按下列方法沿虚线剪下，能使阴影部分的三角形与$\triangle ABC$相似的是(D)

答案： 11.D

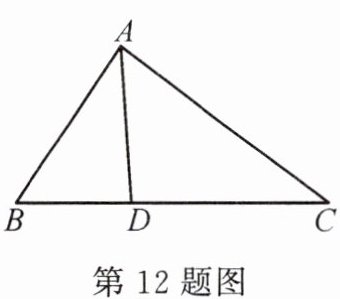
12. 如图，在$\triangle ABC$中，$D$为$BC$上一点，$BC=\sqrt{3}AB = 3BD$，则$AD:AC$的值为\frac{\sqrt{3}}{3}.

答案： $12.\frac{\sqrt{3}}{3}$

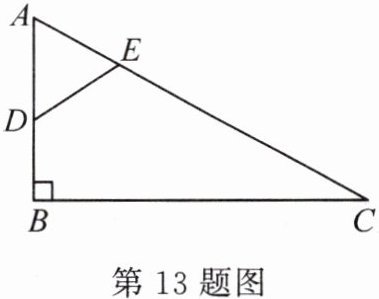
13. 如图，在$\mathrm{Rt}\triangle ABC$中，$\angle B = 90^{\circ}$，$D$为$AB$的中点，点$E$在边$AC$上，$AE=\frac{1}{4}AC$，连结$DE$.若$AC = 4$，则$DE =$1.

答案： 13.1

14. 如图，已知$\angle DAB=\angle ECB$，$\angle ABD=\angle CBE$.求证：
（1）$\triangle ABD\backsim\triangle CBE$；
（2）$\triangle ABC\backsim\triangle DBE$.

答案： 14.（1）证明：
∵∠DAB = ∠ECB,∠ABD = ∠CBE,
∴△ABD∽△CBE.（2）由（1）知,△ABD∽△CBE.
∴$\frac{AB}{CB}=\frac{BD}{BE},$即$\frac{AB}{DB}=\frac{BC}{BE}. $
∵∠ABC = ∠ABD + ∠DBC,∠DBE = ∠DBC + ∠CBE,∠ABD = ∠CBE,
∴∠ABC = ∠DBE. 又
∵$\frac{AB}{DB}=\frac{BC}{BE},$
∴△ABC∽△DBE.

15. 如图，已知$\angle MON = 90^{\circ}$，$A$是$\angle MON$内部的一点，过点$A$作$AB\perp ON$，垂足为$B$，$AB = 3\mathrm{cm}$，$OB = 4\mathrm{cm}$，动点$E$，$F$同时从点$O$出发，点$E$以$1.5\mathrm{cm/s}$的速度沿$ON$方向运动，点$F$以$2\mathrm{cm/s}$的速度沿$OM$方向运动，$EF$与$OA$交于点$C$，连结$AE$，当点$E$到达点$B$时，点$F$随之停止运动.设运动时间为$t\mathrm{s}(t＞0)$.
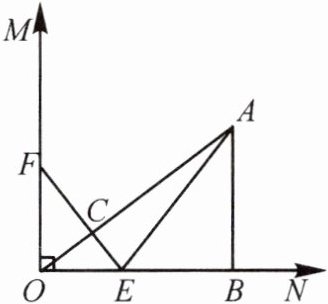
（1）当$t = 1$时，$\triangle EOF$与$\triangle ABO$是否相似？请说明理由；
（2）在运动过程中，不论$t$取何值时，总有$EF\perp OA$，为什么？

答案： 15.（1）△EOF∽△ABO.理由如下：当t = 1时,OE = 1.5 cm,OF = 2 cm.
∵AB = 3 cm,OB = 4 cm,
∴$\frac{OE}{BA}=\frac{OF}{BO}=\frac{1}{2}. $又
∵∠EOF = ∠ABO = 90°,
∴△EOF∽△ABO. （2）在运动过程中,OE = 1.5t cm,OF = 2t cm.
∵AB = 3 cm,OB = 4 cm,
∴$\frac{OE}{BA}=\frac{OF}{BO}. $又
∵∠EOF = ∠ABO = 90°,
∴△EOF∽△ABO.
∴∠EFO = ∠AOB. 又
∵∠AOB + ∠FOC = 90°,
∴∠EFO + ∠FOC = 90°.
∴∠FCO = 90°,即EF⊥OA.