第55页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
10. 在如图所示的象棋盘(各个小正方形的边长均相等)中,根据“马走日”的规则,“马”应落下列哪个位置处,能使“马”“车”“炮”所在位置的格点构成的三角形与“帥”“相”“兵”所在位置的格点构成的三角形相似(
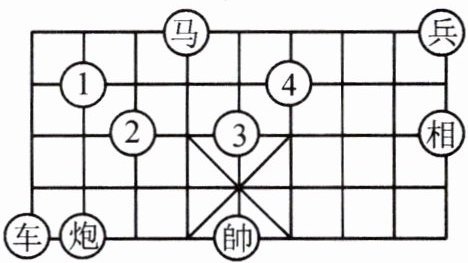
A.①处
B.②处
C.③处
D.④处
B
)
A.①处
B.②处
C.③处
D.④处
答案:
B
11. 如图,在边长为 $1$ 的正方形网格中有点 $P,A,B,C$,则图中所形成的三角形中,相似的三角形是
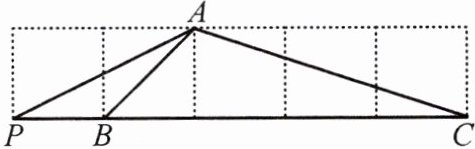
$\triangle APB\sim\triangle CPA$
。
答案:
$\triangle APB\sim\triangle CPA$
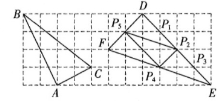
12. 如图,在边长为 $1$ 的小正方形组成的网格中,$\triangle ABC$ 和 $\triangle DEF$ 的顶点都在格点上,$P_1,P_2,P_3,P_4,P_5$ 是 $\triangle DEF$ 边上的 $5$ 个格点,请按要求完成下列各题:
(1) 求证:$\triangle ABC$ 是直角三角形;
(2) 判断 $\triangle ABC$ 和 $\triangle DEF$ 是否相似,并说明理由;
(3) 画一个三角形,使它的顶点为 $P_1,P_2,P_3,P_4,P_5$ 中的 $3$ 个格点,并且与 $\triangle ABC$ 相似。

(1) 求证:$\triangle ABC$ 是直角三角形;
(2) 判断 $\triangle ABC$ 和 $\triangle DEF$ 是否相似,并说明理由;
(3) 画一个三角形,使它的顶点为 $P_1,P_2,P_3,P_4,P_5$ 中的 $3$ 个格点,并且与 $\triangle ABC$ 相似。

答案:
解:
(1)证明:根据勾股定理,得$AB = 2\sqrt{5}$,$AC = \sqrt{5}$,$BC = 5$,$\therefore AB^{2}+AC^{2}=BC^{2}$. $\therefore\triangle ABC$为直角三角形.
(2)$\triangle ABC\sim\triangle DEF$. 理由:根据勾股定理,得$AB = 2\sqrt{5}$,$AC = \sqrt{5}$,$BC = 5$,$DE = 4\sqrt{2}$,$DF = 2\sqrt{2}$,$EF = 2\sqrt{10}$,$\therefore\frac{AB}{DE}=\frac{AC}{DF}=\frac{BC}{EF}=\frac{\sqrt{10}}{4}$.
$\therefore\triangle ABC\sim\triangle DEF$.
(3)
解:
(1)证明:根据勾股定理,得$AB = 2\sqrt{5}$,$AC = \sqrt{5}$,$BC = 5$,$\therefore AB^{2}+AC^{2}=BC^{2}$. $\therefore\triangle ABC$为直角三角形.
(2)$\triangle ABC\sim\triangle DEF$. 理由:根据勾股定理,得$AB = 2\sqrt{5}$,$AC = \sqrt{5}$,$BC = 5$,$DE = 4\sqrt{2}$,$DF = 2\sqrt{2}$,$EF = 2\sqrt{10}$,$\therefore\frac{AB}{DE}=\frac{AC}{DF}=\frac{BC}{EF}=\frac{\sqrt{10}}{4}$.
$\therefore\triangle ABC\sim\triangle DEF$.
(3)

13. 【类比思想】学习“图形的相似”后,我们可以借助探索两个直角三角形全等的条件所获得的经验,继续探索两个直角三角形相似的条件。
(1) “满足一边一锐角对应相等或两直角边对应相等的两个直角三角形全等”,类似地可以得到“满足
(2) “满足斜边和一条直角边对应相等的两个直角三角形全等”,类似地可以得到“满足
请结合下列所给图形,写出已知,并完成说明过程。
已知:如图,
试说明:$Rt\triangle ABC\backsim Rt\triangle A'B'C'$。
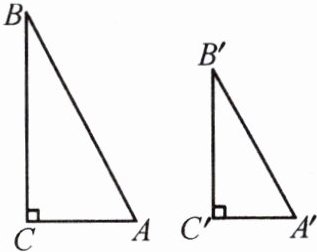
(1) “满足一边一锐角对应相等或两直角边对应相等的两个直角三角形全等”,类似地可以得到“满足
一个锐角对应相等
或两直角边对应成比例
的两个直角三角形相似”;(2) “满足斜边和一条直角边对应相等的两个直角三角形全等”,类似地可以得到“满足
斜边和一条直角边对应成比例
的两个直角三角形相似”。请结合下列所给图形,写出已知,并完成说明过程。
已知:如图,
在$Rt\triangle ABC$和$Rt\triangle A'B'C'$中,$\angle C=\angle C' = 90^{\circ}$,$\frac{AB}{A'B'}=\frac{AC}{A'C'}$
。试说明:$Rt\triangle ABC\backsim Rt\triangle A'B'C'$。

答案:
解:
(1)一个锐角对应相等 两直角边对应成比例
(2)斜边和一条直角边对应成比例 在$Rt\triangle ABC$和$Rt\triangle A'B'C'$中,$\angle C=\angle C' = 90^{\circ}$,$\frac{AB}{A'B'}=\frac{AC}{A'C'}$设$\frac{AB}{A'B'}=\frac{AC}{A'C'}=k(k>0)$,则$AB = kA'B'$,$AC = kA'C'$. 在$Rt\triangle ABC$和$Rt\triangle A'B'C'$中,$\frac{BC}{B'C'}=\frac{\sqrt{AB^{2}-AC^{2}}}{\sqrt{A'B'^{2}-A'C'^{2}}}=\frac{\sqrt{k^{2}A'B'^{2}-k^{2}A'C'^{2}}}{\sqrt{A'B'^{2}-A'C'^{2}}}=k$,$\therefore\frac{AB}{A'B'}=\frac{AC}{A'C'}=\frac{BC}{B'C'}$. $\therefore Rt\triangle ABC\sim Rt\triangle A'B'C'$.
(1)一个锐角对应相等 两直角边对应成比例
(2)斜边和一条直角边对应成比例 在$Rt\triangle ABC$和$Rt\triangle A'B'C'$中,$\angle C=\angle C' = 90^{\circ}$,$\frac{AB}{A'B'}=\frac{AC}{A'C'}$设$\frac{AB}{A'B'}=\frac{AC}{A'C'}=k(k>0)$,则$AB = kA'B'$,$AC = kA'C'$. 在$Rt\triangle ABC$和$Rt\triangle A'B'C'$中,$\frac{BC}{B'C'}=\frac{\sqrt{AB^{2}-AC^{2}}}{\sqrt{A'B'^{2}-A'C'^{2}}}=\frac{\sqrt{k^{2}A'B'^{2}-k^{2}A'C'^{2}}}{\sqrt{A'B'^{2}-A'C'^{2}}}=k$,$\therefore\frac{AB}{A'B'}=\frac{AC}{A'C'}=\frac{BC}{B'C'}$. $\therefore Rt\triangle ABC\sim Rt\triangle A'B'C'$.
查看更多完整答案,请扫码查看


