《2025年名校课堂九年级数学上册华师大版8河南专版》

11. [新考向 真实情境](2023·南阳卧龙区期中)一种燕尾夹如图1所示，图2是在闭合状态时的示意图，图3是在打开状态时的示意图(数据如图，单位：$mm$)，则从闭合到打开，点 $B$，$D$ 之间的距离减少了(A)

A.$25\ mm$
B.$20\ mm$
C.$15\ mm$
D.$8\ mm$

答案： A

12. (2024·南阳名校期中联考)如图，$DE$ 是 $\triangle ABC$ 的中位线，点 $F$ 在 $DB$ 上，$DF = 2BF$，连结 $EF$ 并延长，与 $CB$ 的延长线相交于点 $M$。若 $BC = 6$，则线段 $CM$ 的长为$\frac{15}{2}$。

答案： $\frac{15}{2}$

13. (2024·南阳新野县期中)如图，在平面直角坐标系中，已知点 $E(-4, 2)$，$F(-2, -2)$。若 $\triangle OEF$ 与 $\triangle OE'F'$ 关于点 $O$ 位似，且 $\triangle OEF$ 的面积是 $\triangle OE'F'$ 面积的 $4$ 倍，则点 $E$ 的对应点 $E'$ 的坐标为(D)

A.$(-2, 1)$
B.$(-8, 4)$
C.$(-8, 4)$ 或 $(8, -4)$
D.$(-2, 1)$ 或 $(2, -1)$

答案： D

14. (2023·南阳卧龙区期中)如图，在平面直角坐标系中，$\triangle OAB$ 的顶点坐标分别为 $O(0, 0)$，$A(2, 1)$，$B(1, -2)$。
(1) 以原点 $O$ 为位似中心，在 $y$ 轴的右侧画出 $\triangle OAB$ 的一个位似三角形 $OA_1B_1$，使它与 $\triangle OAB$ 的相似比为 $2:1$；
(2) 画出将 $\triangle OAB$ 先向左平移 $2$ 个单位长度，再向上平移 $1$ 个单位长度后得到的 $\triangle O_2A_2B_2$；
(3) $\triangle OA_1B_1$ 和 $\triangle O_2A_2B_2$ 是位似图形吗？若是，请在图中标出位似中心点 $M$，并写出点 $M$ 的坐标。

答案：

(1)如图
(2)如图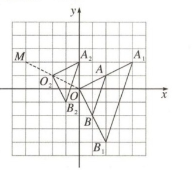
(3)$\triangle OA_1B_1$和$\triangle O_2A_2B_2$是位似图形，点$M$的坐标为$(-4,2)$.

15. 【教材呈现】如图，这是华师版九年级上册数学教材 $66$ 页的部分内容。
【例3】如图1，在 $\triangle ABC$ 中，$DE // BC$，$EF // AB$。求证：$\triangle ADE \backsim \triangle EFC$。
想一想
在例3中，如果点 $D$ 恰好是边 $AB$ 的中点，那么点 $E$ 是边 $AC$ 的中点吗？此时，$DE$ 和 $BC$ 有什么关系？$\triangle ADE$ 与 $\triangle EFC$ 又有什么特殊关系呢？ 
【问题解决】
(1) 请结合图1给出例3的证明过程；
【拓展探究】
(2) 如图2，在 $\triangle ABC$ 中，$D$ 是边 $AB$ 的三等分点，过 $D$ 分别作 $DE // AC$，$DF // BC$ 分别与边 $BC$，$AC$ 相交于点 $E$，$F$。若 $AC = 6$，$BC = 9$，则四边形 $DECF$ 的周长是14或16；
(3) 如图3，在 $\triangle ABC$ 中，$P$ 是边 $BC$ 上的一点，且 $BP:PC = 2:1$，连结 $AP$，取 $AP$ 的中点 $M$，连结 $BM$ 并延长交 $AC$ 于点 $N$。若 $\triangle AMN$ 的面积为 $3$，则 $\triangle PMB$ 的面积为15。

]

答案：
(1)证明：$\because DE// BC$，$\therefore \angle ADE=\angle B$，$\angle AED=\angle C.\because EF// AB$，$\therefore \angle B=\angle EFC.\therefore \angle ADE=\angle EFC.\therefore \triangle ADE\sim\triangle EFC$.
(2)14或16
(3)15