《2025年名校课堂九年级数学上册华师大版8河南专版》

1. 如图，一支铅笔放在圆柱体笔筒中，笔筒的内部底面直径是9 cm，内壁高12 cm，则这只铅笔的长度可能是(D)

A.9 cm
B.12 cm
C.15 cm
D.18 cm

答案： D

2. 如图，有两棵树，一棵高10 m，另一棵高4 m，两树相距8 m.一只小鸟从一棵树的树梢飞到另一棵树的树梢，小鸟至少飞行(B)

A.8 m
B.10 m
C.12 m
D.14 m

答案： B

3. (教材P101练习T2变式)如图，小亮将升旗的绳子拉到旗杆底端，绳子末端刚好接触到地面，然后将绳子末端拉到距离旗杆8 m处，发现此时绳子末端距离地面2 m，求旗杆的高度(滑轮上方的部分忽略不计).
]

答案： 解：过点C作CB⊥AD于点B，则∠ABC=90°，BC=8m.设旗杆的高度为xm，则AC=AD=xm，AB=(x-2)m.在Rt△ABC中，AB²+BC²=AC²，即(x-2)²+8²=x²，解得x=17.答：旗杆的高度为17m.

4. 某项目学习小组为了测量直立在水平地面上的旗杆AB的高度，把标杆DE直立在同一水平地面上(如图).同一时刻测得旗杆和标杆在太阳光下的影长分别是BC=8.72 m，EF=2.18 m.已知点B，C，E，F在同一条直线上，AB⊥BC，DE⊥EF，DE=2.47 m，则AB=9.88m.

答案： 9.88

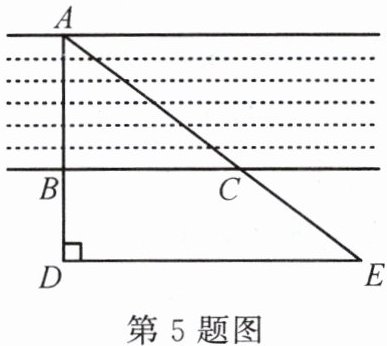
5. 如图，为了估计河的宽度，在河的对岸选定一个目标点A，在近岸取点B，C，D，E，使点A，B，D在一条直线上，且AD⊥DE，点A，C，E也在一条直线上，且DE//BC.如果BC=24 m，BD=12 m，DE=40 m，那么河的宽度AB为18m.

答案： 18

6. (教材P101习题T2变式)(2024·南阳镇平县开学考)如图，某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度，他们通过调整测量位置，使斜边DF与地面保持平行，并使边DE与旗杆顶点A在同一条直线上，已知DE=0.5米，EF=0.4米，测量点D到地面的距离DG=2米，到旗杆的水平距离DC=15米，求旗杆的高度.
]

答案： 解：
∵∠ADC=∠FDE，∠ACD=∠FED=90°，
∴△ACD∽△FED.
∴$\frac{AC}{CD}=\frac{EF}{DE}$，即$\frac{AC}{15}=\frac{0.4}{0.5}$，解得AC=12.
∵AB⊥BG，DG⊥BG，DC⊥AB，
∴∠ABG=∠BGD=∠DCB=90°.
∴四边形BGDC是矩形.
∴BC=DG=2米.
∴AB=AC+BC=12+2=14（米）.答：旗杆的高度为14米.