第71页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
9. 如图,在网格图中,以点 $ O $ 为位似中心,把 $ \triangle ABC $ 缩小到原来的 $ \frac{1}{2} $,则点 $ A $ 的对应点为(
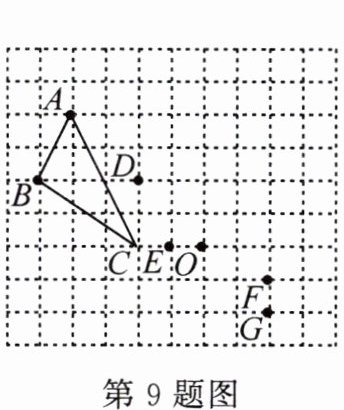
A.点 $ D $
B.点 $ E $
C.点 $ D $ 或点 $ G $
D.点 $ D $ 或点 $ F $
C
)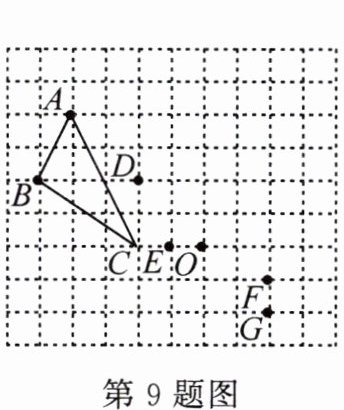
A.点 $ D $
B.点 $ E $
C.点 $ D $ 或点 $ G $
D.点 $ D $ 或点 $ F $
答案:
C
10. 在如图所示的网格中,以点 $ O $ 为位似中心,四边形 $ ABCD $ 的位似图形是(
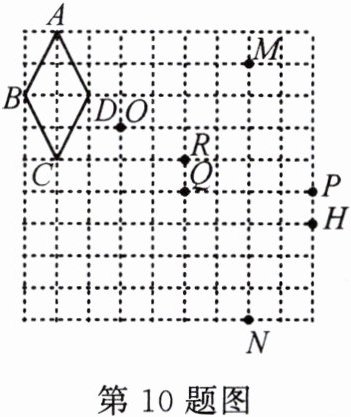
A.四边形 $ NPMQ $
B.四边形 $ NPMR $
C.四边形 $ NHMQ $
D.四边形 $ NHMR $
A
)
A.四边形 $ NPMQ $
B.四边形 $ NPMR $
C.四边形 $ NHMQ $
D.四边形 $ NHMR $
答案:
A
11. 由 $ 12 $ 个有公共顶点 $ O $ 的直角三角形拼成如图所示的图形,$ \angle AOB = \angle BOC = \angle COD = \cdots = \angle LOM = 30^{\circ} $。若 $ S_{\triangle AOB} = 1 $,则图中与 $ \triangle AOB $ 位似的三角形的面积为(

A.$ (\frac{4}{3})^3 $
B.$ (\frac{4}{3})^7 $
C.$ (\frac{4}{3})^6 $
D.$ (\frac{3}{4})^6 $
C
)
A.$ (\frac{4}{3})^3 $
B.$ (\frac{4}{3})^7 $
C.$ (\frac{4}{3})^6 $
D.$ (\frac{3}{4})^6 $
答案:
C
12. 如图,$ \triangle ABC $ 与 $ \triangle A'B'C' $ 是位似图形,点 $ A $,$ B $,$ A' $,$ B' $,$ O $ 共线,点 $ O $ 为位似中心。
(1) $ AC $ 与 $ A'C' $ 平行吗?为什么?

(2) 若 $ AB = 2A'B' $,$ OC' = 5 $,求 $ CC' $ 的长。
(1) $ AC $ 与 $ A'C' $ 平行吗?为什么?

(2) 若 $ AB = 2A'B' $,$ OC' = 5 $,求 $ CC' $ 的长。
答案:
(1)AC//A'C'. 理由如下:
∵△ABC与△A'B'C'是位似图形,
∴△ABC∽△A'B'C',
∴∠A=∠C'A'B'.
∴AC//A'C'.
(2)
∵△ABC∽△A'B'C',
∴$\frac{AB}{A'B'}=\frac{AC}{A'C'}. $
∵AB=2A'B',
∴$\frac{AC}{A'C'}=\frac{AB}{A'B'}=\frac{2}{1}. $又
∵△ABC与△A'B'C'是位似图形,
∴$\frac{OC}{OC'}=\frac{AC}{A'C'}=\frac{2}{1}. $
∴OC'=5,
∴OC=10.
∴CC'=OC-OC'=10-5=5.
(1)AC//A'C'. 理由如下:
∵△ABC与△A'B'C'是位似图形,
∴△ABC∽△A'B'C',
∴∠A=∠C'A'B'.
∴AC//A'C'.
(2)
∵△ABC∽△A'B'C',
∴$\frac{AB}{A'B'}=\frac{AC}{A'C'}. $
∵AB=2A'B',
∴$\frac{AC}{A'C'}=\frac{AB}{A'B'}=\frac{2}{1}. $又
∵△ABC与△A'B'C'是位似图形,
∴$\frac{OC}{OC'}=\frac{AC}{A'C'}=\frac{2}{1}. $
∴OC'=5,
∴OC=10.
∴CC'=OC-OC'=10-5=5.
$13. $如图,在矩形$ ABCD $中,对角线$ AC ,$$ BD $相交于点$ O 。$
$(1) $过点$ O $作$ OE \perp BC $于点$ E ,$连结$ DE $交$ OC $于点$ F ,$作$ FG \perp BC $于点$ G ,$则$ \triangle ABC $与$ \triangle FGC $是位似图形吗$?$若是,请说出位似中心,并求出相似比;若不是,请说明理由;
$(2) $在$(1)$的条件下,连结$ DG $交$ AC $于点$ H ,$作$ HI \perp BC $于点$ I ,$则$ \frac{CI}{BC} $的值为

$(1) $过点$ O $作$ OE \perp BC $于点$ E ,$连结$ DE $交$ OC $于点$ F ,$作$ FG \perp BC $于点$ G ,$则$ \triangle ABC $与$ \triangle FGC $是位似图形吗$?$若是,请说出位似中心,并求出相似比;若不是,请说明理由;
$(2) $在$(1)$的条件下,连结$ DG $交$ AC $于点$ H ,$作$ HI \perp BC $于点$ I ,$则$ \frac{CI}{BC} $的值为
$\frac{1}{4}$
。 
答案:
(1)
∵FG⊥BC,AB⊥BC,
∴FG//AB.
∴∠CFG=∠CAB,∠CGF=∠CBA.
∴△ABC∽△FGC.
∵△ABC与△FGC对应顶点的连线交于点C,对应边互相平行或重合,
∴△ABC与△FGC是位似图形,位似中心是点C.
∵BO=OD,OE//CD,
∴$\frac{DC}{OE}=\frac{BD}{OB}=\frac{BC}{BE}=2. $
∴$\frac{CF}{FO}=\frac{DC}{OE}=2. $
∴$\frac{CF}{OC}=\frac{2}{3}. $
∵OE⊥BC,FG⊥BC,
∴FG//OE.
∴$\frac{CG}{CE}=\frac{CF}{CO}=\frac{2}{3}. $
∴$\frac{CG}{CB}=\frac{1}{3}. $
∴△ABC与△FGC的相似比为$3.(2)\frac{1}{4}$
(1)
∵FG⊥BC,AB⊥BC,
∴FG//AB.
∴∠CFG=∠CAB,∠CGF=∠CBA.
∴△ABC∽△FGC.
∵△ABC与△FGC对应顶点的连线交于点C,对应边互相平行或重合,
∴△ABC与△FGC是位似图形,位似中心是点C.
∵BO=OD,OE//CD,
∴$\frac{DC}{OE}=\frac{BD}{OB}=\frac{BC}{BE}=2. $
∴$\frac{CF}{FO}=\frac{DC}{OE}=2. $
∴$\frac{CF}{OC}=\frac{2}{3}. $
∵OE⊥BC,FG⊥BC,
∴FG//OE.
∴$\frac{CG}{CE}=\frac{CF}{CO}=\frac{2}{3}. $
∴$\frac{CG}{CB}=\frac{1}{3}. $
∴△ABC与△FGC的相似比为$3.(2)\frac{1}{4}$
查看更多完整答案,请扫码查看


