第57页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
5. 新考向 推理能力(2024·南阳南召县期中)图1、图2、图3均是5×4的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1,点A,B,C,D均在格点上.只用无刻度的直尺,在给定的正方形网格中按要求画图,保留作图痕迹,不要求写画法:
(1)如图1,连结AD,BC相交于点E,直接写出$\frac{CE}{BE}$的值为
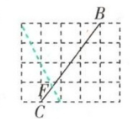
(2)如图2,在BC上找一点F,使BF=4;
(3)如图3,在AC上找一点M,使△ABM的面积为$\frac{8}{5}$,并写出证明.
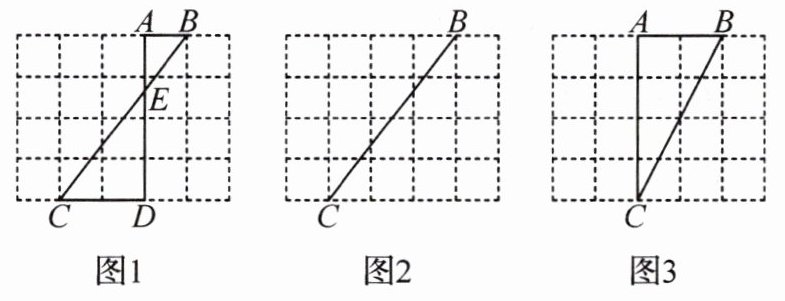
(1)如图1,连结AD,BC相交于点E,直接写出$\frac{CE}{BE}$的值为
2
;(2)如图2,在BC上找一点F,使BF=4;
(3)如图3,在AC上找一点M,使△ABM的面积为$\frac{8}{5}$,并写出证明.

答案:
(1)2
(2)
(3)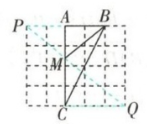
证明:如图3,
连接PQ交AC于点M,连结BM。依题意,得
PA = 2,CQ = 3,AC = 4,AB = 2,AP//CQ,
∴△APM∽△CQM。
∴,
∴AM = MC。
∵AC = AM + MC = MC,AC = 4,
∴MC = 。
∴AM = AC - MC = 4 - = 。
∴。
(1)2
(2)

(3)

证明:如图3,
连接PQ交AC于点M,连结BM。依题意,得
PA = 2,CQ = 3,AC = 4,AB = 2,AP//CQ,
∴△APM∽△CQM。
∴,
∴AM = MC。
∵AC = AM + MC = MC,AC = 4,
∴MC = 。
∴AM = AC - MC = 4 - = 。
∴。
6. (2023·大庆)在综合与实践课上,老师组织同学们以“矩形的折叠”为主题开展数学活动.有一张矩形纸片ABCD如图所示,点N在边AD上,现将矩形折叠,折痕为BN,点A对应的点记为点M.若点M恰好落在边DC上,则图中与△NDM一定相似的三角形是
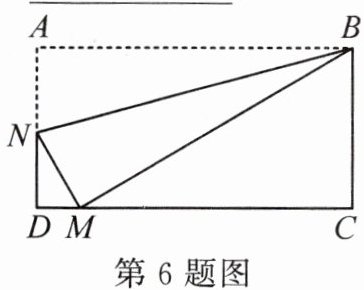
△MCB
.
答案:
△MCB
7. 如图,E是线段BC的中点,∠B=∠C=∠AED,下列结论:①△ABE与△ECD相似;②△ABE与△AED相似;③$\frac{AB}{AE}=\frac{AE}{AD}$;④∠BAE=∠EAD.其中正确的是(
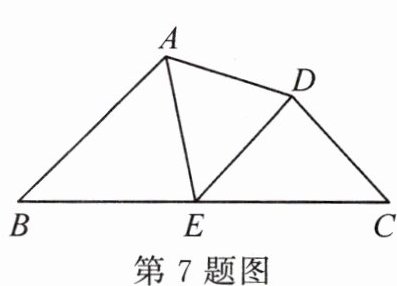
A.①②③④
B.①②③
C.②③④
D.①②④
A
)
A.①②③④
B.①②③
C.②③④
D.①②④
答案:
A
8. (2024·南阳新野县期中)如图,在等边三角形ABC中,BC=6,E是边AB上一点,且BE=2,D是边BC上一动点(E,D两点均不与端点重合),作∠EDF=60°,DF交边AC于点F.
(1)求证:△BED∽△CDF;
(2)连结EF,若EF//BC,求CD的长;
(3)若CF=m,当满足条件的点D有且只有一个时,直接写出m的值.
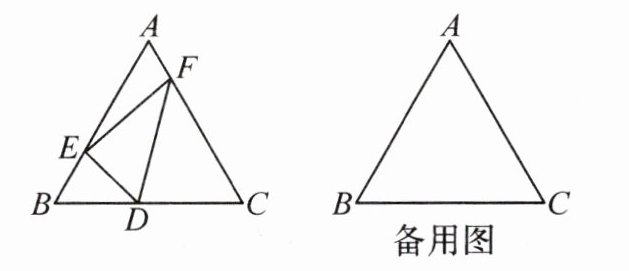
(1)求证:△BED∽△CDF;
(2)连结EF,若EF//BC,求CD的长;
(3)若CF=m,当满足条件的点D有且只有一个时,直接写出m的值.

答案:
(1)证明:
∵△ABC是等边三角形,
∴∠B = ∠C = 60°。
∴∠BED + ∠BDE = 180° - ∠B = 120°。
∵∠EDF = 60°,
∴∠BDE + ∠CDF = 120°。
∴∠BED = ∠CDF。
∴△BED∽△CDF。
(2)
∵△ABC是等边三角形,
∴AB = AC。
∵EF//BC,
∴∠AEF = ∠B = 60°,∠AFE = ∠C = 60°。
∴AE = AF。
∴BE = CF = 2。
∵△BED∽△CDF,
∴$\frac{BE}{CD}=\frac{BD}{CF}$,
∴$\frac{2}{CD}=\frac{6 - CD}{2}$,
∴CD = 3±$\sqrt{5}$。
∴CD的长为3 + $\sqrt{5}$或3 - $\sqrt{5}$。
(3)m = $\frac{9}{2}$。
(1)证明:
∵△ABC是等边三角形,
∴∠B = ∠C = 60°。
∴∠BED + ∠BDE = 180° - ∠B = 120°。
∵∠EDF = 60°,
∴∠BDE + ∠CDF = 120°。
∴∠BED = ∠CDF。
∴△BED∽△CDF。
(2)
∵△ABC是等边三角形,
∴AB = AC。
∵EF//BC,
∴∠AEF = ∠B = 60°,∠AFE = ∠C = 60°。
∴AE = AF。
∴BE = CF = 2。
∵△BED∽△CDF,
∴$\frac{BE}{CD}=\frac{BD}{CF}$,
∴$\frac{2}{CD}=\frac{6 - CD}{2}$,
∴CD = 3±$\sqrt{5}$。
∴CD的长为3 + $\sqrt{5}$或3 - $\sqrt{5}$。
(3)m = $\frac{9}{2}$。
查看更多完整答案,请扫码查看


