《2025年名校课堂九年级数学上册华师大版8河南专版》

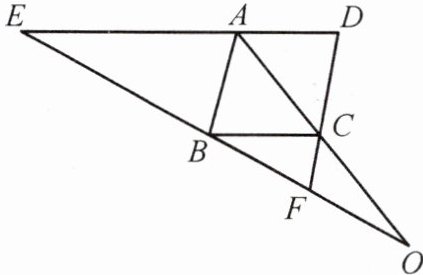
8. 如图，已知 $ ED // BC $，$ \angle EAB = \angle BCF $。求证：
（1）四边形 $ ABCD $ 为平行四边形；
（2）$ OB^{2} = OE \cdot OF $。

答案： 证明：
(1)
∵ED//BC，
∴∠D=∠BCF.
∵∠EAB=∠BCF，
∴∠EAB=∠D.
∴AB//CD.又
∵ED//BC，
∴四边形ABCD为平行四边形.
(2)
∵ED//BC，
∴$\frac{OB}{OE}=\frac{OC}{OA}. $
∵AB//CD，
∴$\frac{OC}{OA}=\frac{OF}{OB}.$
∴$\frac{OB}{OE}=\frac{OF}{OB},$即OB²=OE·OF.

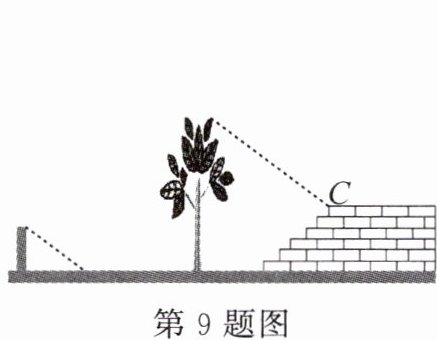
9. (2023·南阳唐河县期中)如图，数学兴趣小组的同学们想利用树影测量树高。课外活动时他们在阳光下测得一根长为 $ 1 \, m $ 的竹竿的影子为 $ 0.9 \, m $，同一时刻测量树高时，发现树的影子不全落在地面上，有一部分影子落在教学楼的台阶上，且影子的末端刚好落在最后一级台阶的上端 $ C $ 处，他们测得落在地面的影长为 $ 1.1 \, m $，台阶总的高度为 $ 1.0 \, m $，台阶水平总宽度为 $ 1.6 \, m $，则树高为(B)

A.$ 3.0 \, m $
B.$ 4.0 \, m $
C.$ 5.0 \, m $
D.$ 6.0 \, m $

答案： B

10. 新考向 真实情境(2023·南阳宛城区期中)如图，在某小区内拐角处的一段道路上，有一儿童在点 $ C $ 处玩耍，一辆汽车从被楼房遮挡的拐角另一侧的 $ A $ 处驶来($ CM \perp DM $，$ BD \perp DM $，$ BC $ 与 $ DM $ 相交于点 $ O $)。已知 $ OM = 4 $ 米，$ CO = 5 $ 米，$ DO = 3 $ 米，$ AO = \sqrt{73} $ 米，则汽车从点 $ A $ 处前行的距离 $ AB = $5.75米时，才能发现点 $ C $ 处的儿童。

答案： 5.75

11. 如图，已知在四边形 $ ABCD $ 中，$ \angle ADB = \angle ACB $，延长 $ AD $，$ BC $ 相交于点 $ E $。求证：
（1）$ \triangle ACE \backsim \triangle BDE $；
（2）$ BE \cdot CD = AB \cdot DE $。

答案： 证明：
(1)
∵∠ADB=∠ACB，
∴∠BDE=∠ACE.又
∵∠CEA=∠DEB，
∴△ACE∽△BDE.
(2)
∵△ACE∽△BDE，
∴$\frac{BE}{AE}=\frac{ED}{EC},$即$\frac{BE}{DE}=\frac{EA}{EC}.$又
∵∠DEC=∠BEA，
∴△ECD∽△EAB.
∴$\frac{BE}{DE}=\frac{AB}{CD},$即BE·CD=AB·DE.

12. （2023·河南）综合实践活动中，某小组用木板自制了一个测高仪测量树高，测高仪 $ ABCD $ 为正方形，$ AB = 30 \, cm $，顶点 $ A $ 处挂了一个铅锤 $ M $。如图，这是测量树高的示意图，测高仪上的点 $ D $，$ A $ 与树顶 $ E $ 在一条直线上，铅垂线 $ AM $ 交 $ BC $ 于点 $ H $。经测量，点 $ A $ 距地面 $ 1.8 \, m $，到树 $ EG $ 的距离 $ AF = 11 \, m $，$ BH = 20 \, cm $，求树 $ EG $ 的高度（结果精确到 $ 0.1 \, m $）。

答案： 解：由题意可知，∠BAE=∠MAF=∠BAD=∠ABC=90°,FG=1.8 m，则∠FAE+∠BAF=∠BAF+∠BAH=90°.
∴∠FAE=∠BAH.
∴△AEF∽△AHB.
∴$\frac{EF}{BH}=\frac{AF}{AB}. $
∵AB=30 cm,BH=20 cm，
∴$\frac{EF}{20}=\frac{11}{30}. $
∴$EF=\frac{22}{3}. $
∴$EG=EF+FG=\frac{22}{3}+1.8≈9.1m.$答：树EG的高度约为9.1m.