第68页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
1. (2024·兰州)如图,小张想估测被池塘隔开的 A,B 两处景观之间的距离,他先在 AB 外取一点 C,然后步测出 AC,BC 的中点 D,E,并步测出 DE 的长约为 18 m,由此估测 A,B 之间的距离为(

A.18 m
B.24 m
C.36 m
D.54 m
C
)
A.18 m
B.24 m
C.36 m
D.54 m
答案:
C
2. (2024·广安)如图,在△ABC 中,D,E 分别是 AC,BC 的中点.若∠A = 45°,∠CED = 70°,则∠C 的度数为(

A.45°
B.50°
C.60°
D.65°
D
)
A.45°
B.50°
C.60°
D.65°
答案:
D
3. 如图,在△ABC 中,D,E 分别是边 AB,BC 的中点.若△DBE 的周长是 6,则△ABC 的周长是(
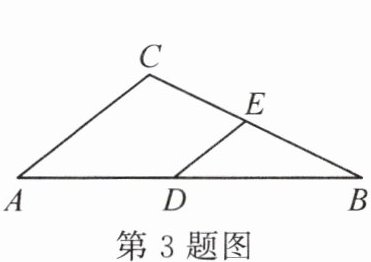
A.8
B.10
C.12
D.14
C
)
A.8
B.10
C.12
D.14
答案:
C
4. (2024·湖南)如图,在△ABC 中,D,E 分别为边 AB,AC 的中点,则下列结论中错误的是(
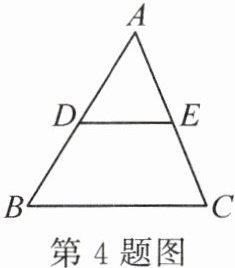
A.DE//BC
B.△ADE∽△ABC
C.BC = 2DE
D.$ S_{△ADE} = \frac{1}{2}S_{△ABC} $
D
)
A.DE//BC
B.△ADE∽△ABC
C.BC = 2DE
D.$ S_{△ADE} = \frac{1}{2}S_{△ABC} $
答案:
D
5. (教材 P80 习题 T3 变式)如图,在四边形 ABCD 中,P 是对角线 BD 的中点,E,F 分别是 AB,CD 的中点,AD = BC,∠FPE = 136°,则∠PFE 的度数是(
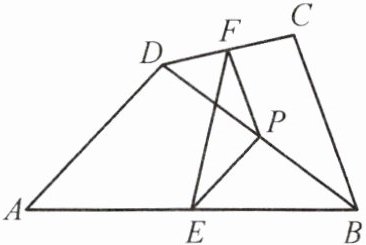
A.15°
B.20°
C.22°
D.44°
C
)
A.15°
B.20°
C.22°
D.44°
答案:
C
6. 如图,在平面直角坐标系中,△AOB 的边 AO,AB 的中点 C,D 的横坐标分别是 1,4,则点 B 的横坐标是
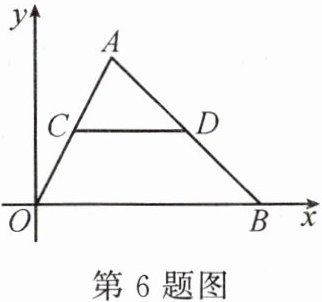
6
.
答案:
6
7. (2024·海南)如图,这是跷跷板的示意图,支柱 OM 经过 AB 的中点 O,OM 与地面 CD 垂直于点 M,OM = 40 cm.当跷跷板的一端 A 着地时,另一端 B 离地面的高度为
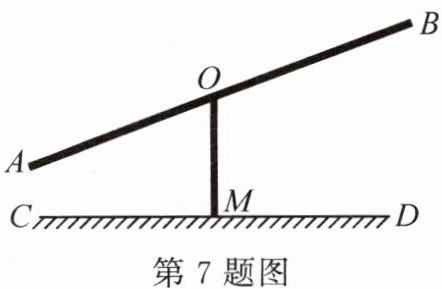
80
cm.
答案:
80
8. 如图,M 是△ABC 的边 BC 的中点,AN 平分∠BAC,BN⊥AN 于点 N,延长 BN 交 AC 于点 D,已知 AB = 10,BC = 15,MN = 3.
(1)求证:BN = DN;
(2)求△ABC 的周长.
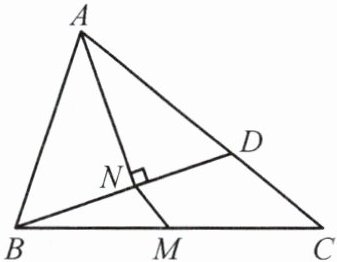
(1)求证:BN = DN;
(2)求△ABC 的周长.

答案:
8.解:
(1)证明:
∵AN平分∠BAC,BN⊥AN,
∴∠BAN = ∠DAN,∠ANB = ∠AND.又
∵AN = AN,
∴△ABN≌△ADN(ASA).
∴BN = DN.
(2)
∵△ABN≌△ADN,
∴AD = AB = 10,BN = DN.又
∵M是BC的中点,
∴MN是△BDC的中位线.
∴CD = 2MN = 6.
∴△ABC的周长为AB + BC + CD + AD = 10 + 15 + 6 + 10 = 41.
(1)证明:
∵AN平分∠BAC,BN⊥AN,
∴∠BAN = ∠DAN,∠ANB = ∠AND.又
∵AN = AN,
∴△ABN≌△ADN(ASA).
∴BN = DN.
(2)
∵△ABN≌△ADN,
∴AD = AB = 10,BN = DN.又
∵M是BC的中点,
∴MN是△BDC的中位线.
∴CD = 2MN = 6.
∴△ABC的周长为AB + BC + CD + AD = 10 + 15 + 6 + 10 = 41.
9. 如图,D 是△ABC 的重心,则下列结论正确的是(
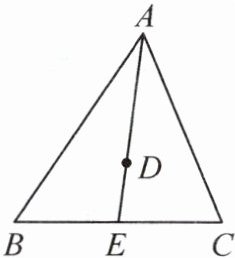
A.2AD = DE
B.AD = 2DE
C.3AD = 2DE
D.AD = 3DE
B
)
A.2AD = DE
B.AD = 2DE
C.3AD = 2DE
D.AD = 3DE
答案:
B
查看更多完整答案,请扫码查看


