第37页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
4. 下图是2024年5月的月历表,用一个方框在表中圈出六个数(如图所示),若圈出的六个数中,最小的数与最大的数的乘积为136,求这个最小的数(请用方程知识解答).


答案:
设这个最小的数为$x$,则最大的数为$x+9$.依题意,得$x(x+9)=136$,解得$x_1=8$,$x_2=-17$(不符合题意,舍去).答:这个最小的数为8.
5. 某农场要建一个饲养场(矩形ABCD),两面靠墙(AD位置的墙最大可用长度为25m,AB位置的墙最大可用长度为21m),另外两边用木栏围成,中间用木栏隔成两个小矩形,并在如图所示的两处各留1m宽的门(不用木栏),建成后木栏总长为50m.
(1) 若饲养场(矩形ABCD)的面积为240m²,求边CD的长;

(2) 小芳说:“饲养场的面积能达到400m².”若能达到,求出边CD的长;若不能达到,请说明理由.
(1) 若饲养场(矩形ABCD)的面积为240m²,求边CD的长;

(2) 小芳说:“饲养场的面积能达到400m².”若能达到,求出边CD的长;若不能达到,请说明理由.
答案:
(1)设$CD=xm$,则$AD=(50-2x+2)m$.由题意,得$x(50-2x+2)=240$,解得$x_1=6$,$x_2=20$.当$x=6$时,$50-2×6+2=40>25$,不符合题意,舍去;当$x=20$时,$50-2×20+2=12<25$,符合题意.$\therefore$边$CD$的长为$20m$.
(2)不能.理由如下:由题意,得$x(50-2x+2)=400$,整理,得$x^2-26x+200=0$.$\because \Delta=(-26)^2-4×1×200=-124<0$,$\therefore$该方程无解.$\therefore$饲养场的面积不能达到$400m^2$.
(1)设$CD=xm$,则$AD=(50-2x+2)m$.由题意,得$x(50-2x+2)=240$,解得$x_1=6$,$x_2=20$.当$x=6$时,$50-2×6+2=40>25$,不符合题意,舍去;当$x=20$时,$50-2×20+2=12<25$,符合题意.$\therefore$边$CD$的长为$20m$.
(2)不能.理由如下:由题意,得$x(50-2x+2)=400$,整理,得$x^2-26x+200=0$.$\because \Delta=(-26)^2-4×1×200=-124<0$,$\therefore$该方程无解.$\therefore$饲养场的面积不能达到$400m^2$.
$6. 【$问题提出$】$九$(1)$班共有$56$名同学,若每两名同学之间仅通过一次视频电话,如何求全班$56$名同学共通过多少次视频电话呢$?$
$【$模型构建$】$用点$M_{1},M_{2},M_{3},...,M_{56}$分别表示第$1,$$2,$$3,$$…,$$56$名同学,把该班人数$n$与视频通话次数$S$之间的关系用如图所示的模型表示:
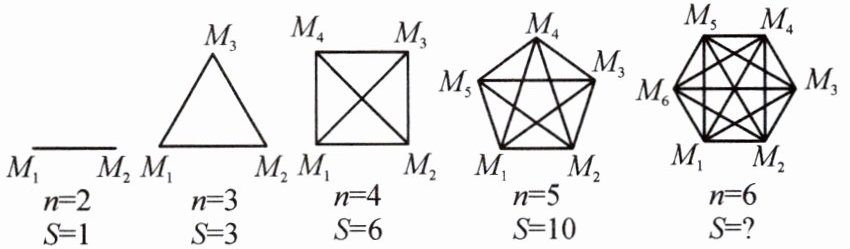
$【$问题解决$】$
$(1) $上图中,当$n=6$时,$S$的值为
$(2) $通过探索发现,通电话次数$S$与该班级人数$n$之间的关系式为
$(3) $若该班全体女生相互之间共视频通话$253$次,则该班有多少名女生$?$
$【$模型构建$】$用点$M_{1},M_{2},M_{3},...,M_{56}$分别表示第$1,$$2,$$3,$$…,$$56$名同学,把该班人数$n$与视频通话次数$S$之间的关系用如图所示的模型表示:

$【$问题解决$】$
$(1) $上图中,当$n=6$时,$S$的值为
$15$
; $(2) $通过探索发现,通电话次数$S$与该班级人数$n$之间的关系式为
$S=\frac{n(n-1)}{2}$
,则当$n=56$时,对应的$S=$ $1540$
; $(3) $若该班全体女生相互之间共视频通话$253$次,则该班有多少名女生$?$
答案:
(1)15
(2)$S=\frac{n(n-1)}{2}$ 1540
(3)设该班有$x$名女生.依题意,得$\frac{x(x-1)}{2}=253$.解得$x_1=23$,$x_2=-22$(不符合题意,舍去).答:该班有23名女生.
(1)15
(2)$S=\frac{n(n-1)}{2}$ 1540
(3)设该班有$x$名女生.依题意,得$\frac{x(x-1)}{2}=253$.解得$x_1=23$,$x_2=-22$(不符合题意,舍去).答:该班有23名女生.
查看更多完整答案,请扫码查看


