《2025年名校课堂九年级数学上册华师大版8河南专版》

11. 如图，在$\triangle ABC$中，点$D$，$E$分别在$AB$，$AC$上，$AF$平分$\angle BAC$交$DE$于点$G$。若$AE=3$，$EC=1$，$AD=2$，$BD=4$，则$AG:AF=$(B)

A.$2:5$
B.$1:2$
C.$1:3$
D.$3:5$

答案： B

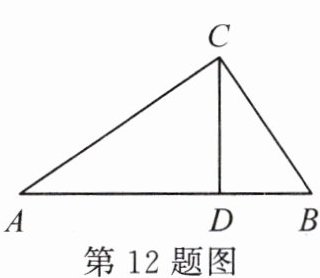
$12. (2023·$郑州管城区月考$)$如图，在$Rt \triangle ABC$中，$\angle ACB=90^{\circ}，$$CD \perp AB，$垂足为$D。$如果$\frac{C_{\triangle ADC}}{C_{\triangle CDB}}=\frac{3}{2}，$$AD=8，$那么$CD$的长是　　$\frac{16}{3}$　　。　　

答案： $\frac{16}{3}$

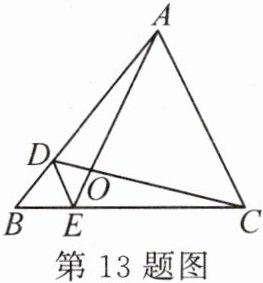
$13. $如图所示，$D，$$E$分别是$\triangle ABC$的边$AB，$$BC$上的点，$DE // AC。$若$S_{\triangle BDE}:S_{\triangle CDE}=1:3，$则$S_{\triangle BDE}:S_{四边形DECA}$的值为　　$\frac{1}{15}$　　。　　

答案： $\frac{1}{15}$

14. （2024·南阳名校期中联考）如图，$F$是平行四边形$ABCD$的边$AD$上一点，直线$CF$交线段$BA$的延长线于点$E$。
（1）求证：$\triangle AEF \backsim \triangle DCF$；
（2）$AF:DF=1:2$，$AE=\sqrt{2}$，$S_{\triangle AEF}=\frac{2}{3}$。
①求$AB$的长；
②求$\triangle EBC$的面积。

答案： 解：
(1)证明：$\because$四边形ABCD是平行四边形，$\therefore BA// CD.\therefore \angle E = \angle FCD,\angle EAF = \angle CDF.\therefore \triangle AEF\sim \triangle DCF$.
(2)①由
(1)知，$\triangle AEF\sim \triangle DCF,\therefore \frac{AE}{DC} = \frac{AF}{DF}.\because AF:DF = 1:2,AE = \sqrt{2},\therefore \frac{\sqrt{2}}{DC} = \frac{1}{2}\therefore DC = 2\sqrt{2}.\because$四边形ABCD是平行四边形，$\therefore AB = DC = 2\sqrt{2}$. ②$\because$四边形ABCD是平行四边形，$\therefore AD// BC.\therefore \triangle EAF\sim \triangle EBC.\therefore \frac{S_{\triangle EAF}}{S_{\triangle EBC}} = (\frac{EA}{EB})^2.\because S_{\triangle AEF} = \frac{2}{3},AB = 2\sqrt{2},AE = \sqrt{2},\therefore EB = EA + AB = 3\sqrt{2}.\therefore \frac{EA}{EB} = \frac{\sqrt{2}}{3\sqrt{2}} = \frac{1}{3}.\therefore \frac{\frac{2}{3}}{S_{\triangle EBC}} = (\frac{1}{3})^2\therefore S_{\triangle EBC} = 6$.

15. （2023·郑州十一中月考）探究发现：
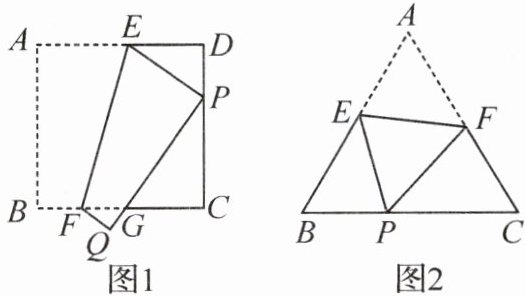
（1）如图1，将一张正方形纸片$ABCD$折叠，使顶点$A$落在边$CD$上的点$P$处（点$P$与点$C$，$D$不重合），折痕为$EF$，折叠后边$AB$落在$PQ$的位置，$PQ$与$BC$交于点$G$。若$DP=1$，$CP=4$，求$CG$的长；
实践应用：
（2）如图2，将边长为$5$的等边三角形纸片$ABC$折叠，使顶点$A$落在边$BC$上的点$P$处（点$P$与点$B$，$C$不重合），折痕为$EF$，当点$P$在边$BC$的什么位置时，$\triangle BEP$与$\triangle CPF$的面积比是$9:25$？请写出求解过程。

答案： 解：
(1)由折叠的性质知，$AE = EP,\angle A = \angle EPG.\because CP = 4,DP = 1,\therefore CD = AD = 5$. 设$ED = x$，则$AE = EP = 5 - x$. 在$Rt\triangle DEP$中，$EP^2 = ED^2 + PD^2,\therefore (5 - x)^2 = x^2 + 1$,解得$x = 2.4.\therefore ED = 2.4.\because$四边形ABCD是正方形，$\therefore \angle EDP = \angle C = \angle A = \angle EPG = 90°.\therefore \angle DEP + \angle EPD = 90°,\angle EPD + \angle CPG = 90°.\therefore \angle DEP = \angle CPG.\therefore \triangle DEP\sim \triangle CPG.\therefore \frac{DP}{CG} = \frac{DE}{CP}.\therefore CG = \frac{DP\cdot CP}{DE} = \frac{5}{3}$.
(2)由折叠的性质知，$\angle A = \angle EPF,AE = PE,AF = PF.\because \triangle ABC$是等边三角形，$\therefore \angle A = \angle B = \angle C = 60°,AB = BC = CA = 5.\therefore \angle B = \angle EPF.\because \angle B + \angle BEP = \angle EPC,\angle EPC = \angle EPF + \angle FPC,\therefore \angle BEP = \angle FPC.\therefore \triangle BEP\sim \triangle CPF.\because \triangle BEP\sim \triangle CPF,\triangle BEP$与$\triangle CPF$面积的比是$9:25,\therefore PE:PF = 3:5$. 设$PE = 3x$，则$AE = 3x,PF = AF = 5x.\therefore BE = AB - AE = 5 - 3x,FC = AC - AF = 5 - 5x.\because \triangle BEP\sim \triangle CPF,\therefore \frac{BP}{FC} = \frac{BE}{PC} = \frac{PE}{PF} = \frac{3}{5}\therefore BP = \frac{3}{5}FC = \frac{3}{5}(5 - 5x) = 3 - 3x.\therefore BP = 3 - 3x = 3 - 3× \frac{19}{24} = \frac{5}{8}.\because BP:BC = \frac{5}{8}:5 = \frac{1}{8},\therefore BP = \frac{1}{8}BC.\therefore$当点P在边BC的$\frac{1}{8}$处且靠近点B时，$\triangle BEP$与$\triangle CPF$的面积比是$9:25$.