《2025年名校课堂九年级数学上册华师大版8河南专版》

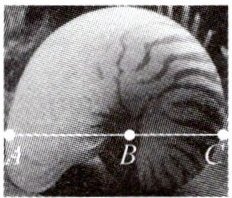
1. (2024·南阳期中)黄金分割被很多人认为是“最美比例”，是因为它符合人们的视觉习惯和审美心理，能够创造出更加和谐、平衡和美观的艺术作品和产品。在自然界中黄金分割也很常见，如图，这是一个有着“最美比例”的鹦鹉螺，点 B 是线段 AC 的黄金分割点，AB＞BC。若 AC=10 cm，则 AB 的长约为(B)

A.0.618 cm
B.6.18 cm
C.3.82 cm
D.0.382 cm

答案： B

2. 宽与长的比是$\frac{\sqrt{5}-1}{2}$(约为 0.618)的矩形叫做黄金矩形。黄金矩形给我们以协调、匀称的美感，世界各国许多著名的建筑，为取得最佳的视觉效果，都采用了黄金矩形的设计，如希腊的帕特农神庙(图 1)。下面我们折叠出一个黄金矩形：
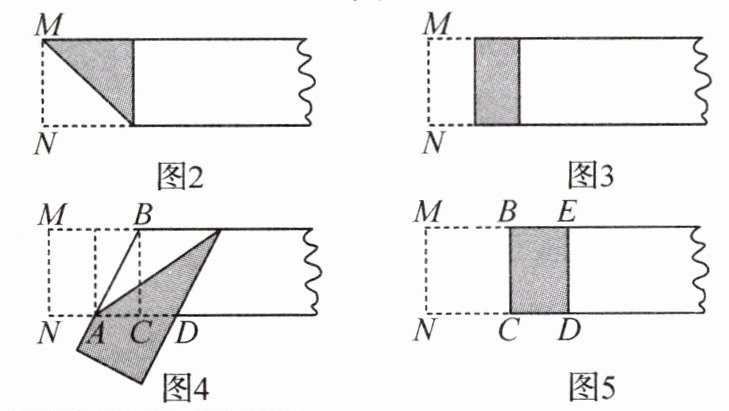
第一步，在宽 MN 为 2 的矩形纸片的一端，利用图 2 的方法折出一个正方形，然后把纸片展平。
第二步，如图 3，把这个正方形对折成两个全等的矩形，再把纸片展平。
第三步，折出内侧矩形的对角线 AB，并把 AB 折到如图 4 所示的 AD 处，此时，AB=，CD=。
第四步，展平纸片，按照所得的点 D 折出 DE，矩形 BCDE(图 5)就是黄金矩形。原因是。

答案： $\sqrt{5}$，$\sqrt{5}-1$，$\frac{CD}{BC}=\frac{\sqrt{5}-1}{2}$

$3. $新考向$ $跨学科$(2024·$山西$)$黄金分割是汉字结构最基本的规律。借助如图所示的正方形习字格书写的汉字$“$晋$”$端庄稳重、舒展美观。已知一条分割线的端点$ A，$$B $分别在习字格的边$ MN，$$PQ $上，且$ AB//NP，$$“$晋$”$字的笔画$“㇔”$的位置在$ AB $的黄金分割点$ C $处，且$\frac{BC}{AB}=\frac{\sqrt{5}-1}{2}。$若$ NP=2 cm，$则$ BC=$　　$(\sqrt{5}-1)$　　$cm($结果保留根号$)。$　　

答案： $(\sqrt{5}-1)$

4. 小明同学探究学习以下内容：“一个点把一条线段分为两段，如果其中较长的一段与整条线段的比等于较短一段与较长一段的比，我们就说这个点是这条线段的黄金分割点，较长的一段与整条线段的比值（或较短一段与较长一段的比值）叫做黄金分割数，即$\frac{\sqrt{5}-1}{2}\approx0.618$。”
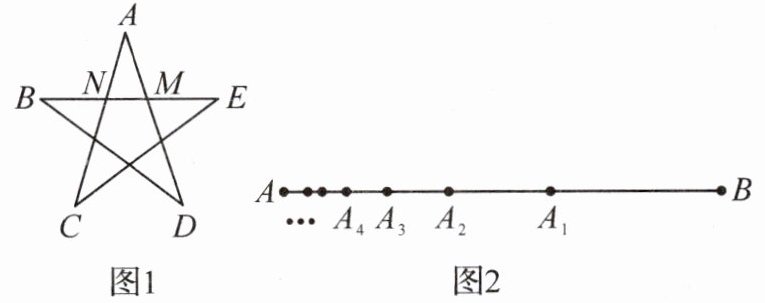
探究发现：在现实生活中，黄金分割无处不在。如图 1，我国国旗上的正五角星也存在黄金分割点，如：$\frac{MN}{NB}=\frac{BN}{BM}=\frac{BM}{BE}=\frac{\sqrt{5}-1}{2}$。
问题解决：
(1)如图 2，已知线段 AB 的长为 1，线段 AB 上的点$A_1$满足关系式$AA_1^2=A_1B\cdot AB$。请计算$AA_1$的长，并判断$AA_1$的长是否为黄金分割数；
(2)在(1)的基础上，若在线段$AA_1$上再取一个点$A_2$，满足$AA_2^2=A_2A_1\cdot AA_1$；在线段$AA_2$上取一点$A_3$，满足$AA_3^2=A_3A_2\cdot AA_2$；……；在线段$AA_{n - 1}$上取一点$A_n$，满足$AA_n^2=A_nA_{n - 1}\cdot AA_{n - 1}$。请直接写出$AA_n$的长。

答案：
(1)设$AA_{1}=x,$则$A_{1}B=1-x.\because AA_{1}^{2}=A_{1}B\cdot AB,\therefore x^{2}=(1-x)×1,$解得$x=\frac{\sqrt{5}-1}{2}$或$x=\frac{-\sqrt{5}-1}{2}($不符合题意,舍去$).\therefore$
$AA_{1}$的长为黄金分割数$.(2)AA_{n}=(\frac{\sqrt{5}-1}{2})^{n}.$