第79页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
7. 如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,那么小巷的宽度为(
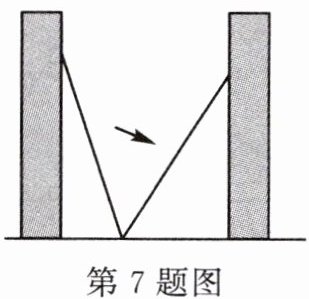
A.2.2米
B.2.3米
C.2.4米
D.2.5米
A
)
A.2.2米
B.2.3米
C.2.4米
D.2.5米
答案:
A
8. 如图,小明在A时测得直立于地面的某树的影长为3米,B时又测得该树的影长为12米.若两次日照的光线互相垂直,则树的高度为
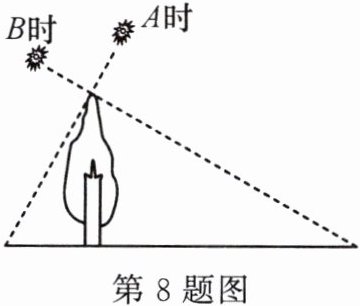
6
米.
答案:
6
9. 如图,光源L与地面的距离LN为8米,与正方体大箱顶的距离LM为2米.已知箱子的棱长DG为6米,在光源照射下,箱子在左侧的影子BE长5米,则箱子在右侧的影子CF的长为

13
米.
答案:
13
10. 新考向 数学文化 清朝《数理精蕴》里有一首小诗《古色古香方城池》:“今有一座古方城,四面正中都开门,南门直行八里止,脚下有座塔耸立.又出西门二里停,切城角恰见塔形,请问诸君能算者,方城每边长是几?”如图所示,诗的意思是有正方形的城池一座,四面城墙的正中有门,从南门口(点D)直行8里有一塔(点A),自西门(点E)直行2里至点B,刚好从切城角(点C)可以看见塔,则这座方城每面城墙的长是

8
里.
答案:
8
11. (教材P102习题T3变式)如图,在一棵树上距地面5米高的B处有三只猴子,第一只猴子爬下树走到离树10米的池塘A处,第二只猴子直接从B处跃到A处,第三只爬到树顶D后直接跃到A处,距离以直线计算,假设其中两只猴子所经过的距离相等.
(1)求第二只猴子经过的直线距离;
(2)求这棵树的高度.
(1)求第二只猴子经过的直线距离;
(2)求这棵树的高度.

答案:
解:
(1)由题意,知在Rt△ABC中,BC=5米,AC=10米,由勾股定理,得BA=$\sqrt{BC^{2}+AC^{2}}$=$5\sqrt{5}$.故第二只猴子经过的直线距离是$5\sqrt{5}$米.
(2)由题意,知AD+DB=BC+CA,且CA=10米,BC=5米,设BD=x,则AD=15-x.在Rt△ACD中,CD²+CA²=AD²,即$(5+x)^{2}+10^{2}=(15-x)^{2}$,解得x=2.5.
∴CD=5+x=7.5.答:这棵树的高度为7.5米.
(1)由题意,知在Rt△ABC中,BC=5米,AC=10米,由勾股定理,得BA=$\sqrt{BC^{2}+AC^{2}}$=$5\sqrt{5}$.故第二只猴子经过的直线距离是$5\sqrt{5}$米.
(2)由题意,知AD+DB=BC+CA,且CA=10米,BC=5米,设BD=x,则AD=15-x.在Rt△ACD中,CD²+CA²=AD²,即$(5+x)^{2}+10^{2}=(15-x)^{2}$,解得x=2.5.
∴CD=5+x=7.5.答:这棵树的高度为7.5米.
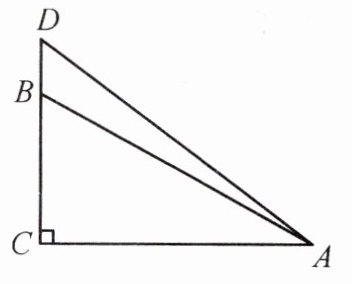
12. 如图所示,在与某建筑物CE相距4 m处有一棵树AB,在某时刻,1.2 m长的竹竿垂直地面,影长为2 m,此时,树的影子有一部分映在地面上,还有一部分影子映在建筑物的墙上.如果墙上的影高DC为2 m,那么这棵树的高度为多少米?
 ]
]
 ]
]
答案:
解:(方法一)过D作DF⊥AB于点F,则DF=BC=4m,BF=DC=2m.依题意,得$\frac{AF}{DF}=\frac{1.2}{2}$,即$\frac{AF}{4}=\frac{1.2}{2}$,解得AF=2.4.
∴AB=AF+BF=2.4+2=4.4(m).答:这棵树的高度为4.4m.
(方法二)延长AD,BC交于点H.依题意,得$\frac{DC}{CH}=\frac{1.2}{2}$,解得CH=$\frac{10}{3}$.
∴BH=$\frac{22}{3}$m.根据△ABH∽△DCH,可得AB=4.4m.
∴AB=AF+BF=2.4+2=4.4(m).答:这棵树的高度为4.4m.
(方法二)延长AD,BC交于点H.依题意,得$\frac{DC}{CH}=\frac{1.2}{2}$,解得CH=$\frac{10}{3}$.
∴BH=$\frac{22}{3}$m.根据△ABH∽△DCH,可得AB=4.4m.
查看更多完整答案,请扫码查看


