《2025年名校课堂九年级数学上册华师大版8河南专版》

7. 某店销售一批户外帐篷，经调查，每顶帐篷利润为200元时，平均每天可售出60顶；单价每降价10元，每天可多售出4顶。已知该店要想平均每天盈利12160元，可列方程为$(200 - x)(60+\frac{x}{10}×4)=12160$，则下列表述正确的是(C)

A.每顶帐篷单价为$x$元
B.降价后平均每天可出售$(200 - x)$顶
C.每顶帐篷单价应降价$x$元
D.降价后每顶帐篷利润为$(60+\frac{x}{10}×4)$元

答案： 7.C

8. “读书可以让人保持思想活力，让人得到智慧启发，让人滋养浩然之气。”某校为响应我市全民阅读活动，利用节假日面向社会开放学校图书馆。据统计，第一个月进馆128人次，进馆人次逐月增加，到第三个月末累计进馆608人次，若进馆人次的月平均增长率相同。
(1)求进馆人次的月平均增长率；
(2)因条件限制，学校图书馆每月接纳能力不超过500人次，在进馆人次的月平均增长率不变的条件下，校图书馆能否接纳第四个月的进馆人次？并说明理由。

答案： $8.$解：　　
$(1)$设进馆人次的月平均增长率为$x，$由题意，得$128+128(1+x)+128(1+x)^2=608.$化简，得$4x^2+12x-7=0.$解得$x_1=0.5=50\%，$$x_2=-3.5($舍去$).$答：进馆人次的月平均增长率为$50\%.$　　
$(2)$能$.$理由：　　
∵第四个月的进馆人次为$128×(1+50\%)^3=432<500，$　　
∴校图书馆能接纳第四个月的进馆人次$. $　　

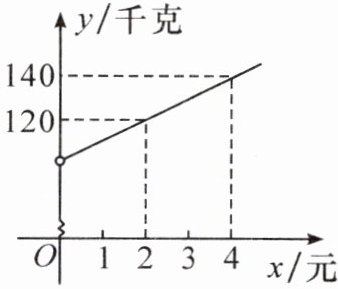
9. (2024·南阳期中)安顺市某商贸公司以每千克40元的价格购进一种干果，计划以每千克60元的价格销售，为了让顾客得到更大的实惠，现决定降价销售，已知这种干果销售量$y$(千克)与每千克降价$x$(元)($0 ＜ x ＜ 20$)之间满足一次函数关系，其图象如图所示。
(1)求$y$与$x$之间的函数关系式；
(2)若该商贸公司要想获利2090元，则这种干果每千克应降价多少元？

答案： 9.解：
(1)设y与x之间的函数关系式为y=kx+b(k≠0)，则$\begin{cases}2k+b=120,\\4k+b=140,\end{cases}$解得$\begin{cases}k=10,\\b=100.\end{cases}$
∴y与x之间的函数关系式为y=10x+100(0＜x＜20).
(2)由题意，得(60-40-x)(10x+100)=2090，整理，得$x^2-10x+9=0.$解得$x_1=1，$$x_2=9.$
∵让顾客得到更大的实惠，
∴x=9.答：若该商贸公司要想获利2090元，则这种干果每千克应降价9元.

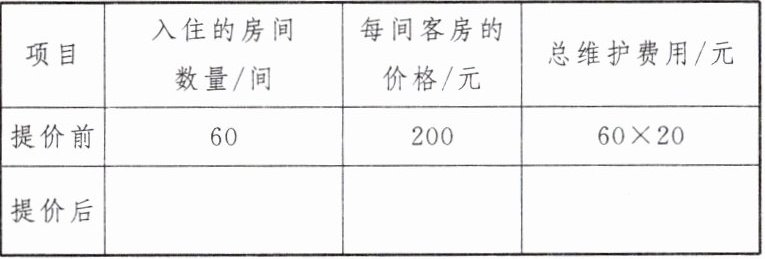
10. 某青年旅社有60间客房供游客居住，在旅游旺季，当每间客房的定价为每天200元时，所有客房都可以住满。每间客房的定价每提高10元，就会有1个客房空闲，对有游客入住的客房，旅社还需要对每个房间支出20元/天的维护费用。设每间客房的定价提高了$x$元。
(1)填表(不需化简)：

(2)若该青年旅社希望每天的纯收入为14000元，且能吸引更多的游客，则每间客房的定价应为多少元？(纯收入=总收入-维护费用)

答案： 10.解：$(1)60-\frac{x}{10} 200+x (60-\frac{x}{10})×20 (2)200×60=12000＜14000，$依题意，得$(200+x)(60-\frac{x}{10})-(60-\frac{x}{10})×20=14000，$解得$x_1=320，$$x_2=100.$当x=320时，$60-\frac{x}{10}=28；$当x=100时，$60-\frac{x}{10}=50.$
∴当x=100时，能吸引更多的游客，则每个房间的定价为200+100=300(元).答：每间客房的定价应为300元.