第9页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. 把$\triangle ABC$经过下列变形,与$\triangle ABC$一定相似的是(
A.各边长都加2
B.各边长都减2
C.各边长都乘以2
D.各边长都平方
C
)A.各边长都加2
B.各边长都减2
C.各边长都乘以2
D.各边长都平方
答案:
C
2. 如图,正方形网格中相似的两个三角形是(

A.①与②
B.①与③
C.③与④
D.②与③
B
)
A.①与②
B.①与③
C.③与④
D.②与③
答案:
B[提示:设每个小正方形的边长为1,图形①的三边为2,√10,√2;图形②的三边为3,√5,√2;图形③的三边为2,2√2,2√5;图形④的三边为3,√2,√17.
∵2/(2√2)=√10/(2√5)=√2/2,
∴①与③相似.]
∵2/(2√2)=√10/(2√5)=√2/2,
∴①与③相似.]
3. 如图,在$8×4$的网格中,每个小正方形的边长都是1,若$\triangle ABC$的三个顶点在图中相应的格点上,图中点$D$、点$E$、点$F$也都在格点上,则下列与$\triangle ABC$相似的三角形是(
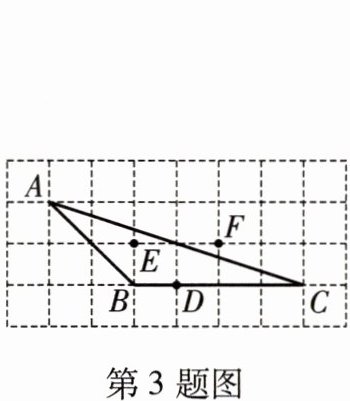
A.$\triangle ACD$
B.$\triangle ADF$
C.$\triangle BDF$
D.$\triangle CDE$
C
)
A.$\triangle ACD$
B.$\triangle ADF$
C.$\triangle BDF$
D.$\triangle CDE$
答案:
C[提示:由网格可知AB=2√2,BC=4,AC=2√10,BD=1,DF=√2,BF=√5,则BD/AB=DF/BC=BF/AC=√2/4,故与△ABC相似的三角形是△BDF.]
4. 如图,棋盘上有$A$,$B$,$C三个黑子与P$,$Q$两个白子. 若要使得$\triangle ABC\backsim\triangle RPQ$,第三个白子$R$应放在(

A.甲
B.乙
C.丙
D.丁
D
)
A.甲
B.乙
C.丙
D.丁
答案:
D
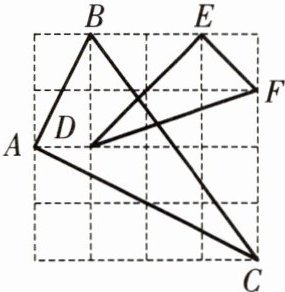
5. 如图,$\triangle ABC和\triangle EFD$的顶点都在正方形网格的格点上,则$\triangle ABC与\triangle EFD$相似吗?请说明理由.

答案:
解:△ABC与△EFD相似.理由如下:
∵AB=√(1 + 4)=√5,AC=√(4 + 16)=2√5,BC=√(9 + 16)=5,EF=√(1 + 1)=√2,ED=√(4 + 4)=2√2,DF=√(1 + 9)=√10,
∴AB/EF=√10/2=AC/DE=BC/DF,
∴△ABC∽△EFD.
∵AB=√(1 + 4)=√5,AC=√(4 + 16)=2√5,BC=√(9 + 16)=5,EF=√(1 + 1)=√2,ED=√(4 + 4)=2√2,DF=√(1 + 9)=√10,
∴AB/EF=√10/2=AC/DE=BC/DF,
∴△ABC∽△EFD.
6. 若$\triangle ABC的每条边长增加各自的10\%得到\triangle A'B'C'$,则$\angle B'的度数与其对应角\angle B$的度数相比(
A.增加了$10\%$
B.减少了$10\%$
C.增加了$(1 + 10\%)$
D.没有改变
D
)A.增加了$10\%$
B.减少了$10\%$
C.增加了$(1 + 10\%)$
D.没有改变
答案:
D
7. 如图,$\triangle ABC和\triangle DBA$在边长为1个单位的方格纸中,它们的顶点在小正方形的顶点位置. 求证:$\angle BAC= \angle BDA$.


答案:
证明:
∵AB=√5,BC=1,AC=√2,BD=5,AD=√10,
∴AB/BD=√5/5,BC/AB=1/√5=√5/5,AC/DA=√2/√10=√5/5,
∴AB/BD=BC/AB=AC/DA,
∴△ABC∽△DBA,
∴∠BAC=∠BDA.
∵AB=√5,BC=1,AC=√2,BD=5,AD=√10,
∴AB/BD=√5/5,BC/AB=1/√5=√5/5,AC/DA=√2/√10=√5/5,
∴AB/BD=BC/AB=AC/DA,
∴△ABC∽△DBA,
∴∠BAC=∠BDA.
8. 如图,已知$O是\triangle ABC$内一点,$D$,$E$,$F分别是OA$,$OB$,$OC$的中点. 求证:$\triangle ABC\backsim\triangle DEF$.


答案:
证明:
∵D,E,F分别是OA,OB,OC的中点,
∴DE=1/2AB,EF=1/2BC,DF=1/2AC,
∴DE/AB=EF/BC=DF/AC,
∴△ABC∽△DEF.
∵D,E,F分别是OA,OB,OC的中点,
∴DE=1/2AB,EF=1/2BC,DF=1/2AC,
∴DE/AB=EF/BC=DF/AC,
∴△ABC∽△DEF.
查看更多完整答案,请扫码查看


