《2025年全科王同步课时练习九年级数学上册青岛版》

1. (2023·东营垦利区校级月考)如图,在综合实践活动中,小明在学校门口的点$C处测得树的顶端A的仰角为37^{\circ}$,同时测得$BC = 20m$,则树的高$AB$(单位：$m$)为(A)


A.$20\tan37^{\circ}$
B.$\dfrac{20}{\tan37^{\circ}}$
C.$\dfrac{20}{\sin37^{\circ}}$
D.$20\sin37^{\circ}$

答案： A

2. 如图,建筑物$BC的顶部竖直立有一个广告牌AB$,从距离建筑物$15m的D处测得广告牌的顶部A的仰角为39^{\circ}$,测得广告牌的底部$B的仰角为30^{\circ}$,求广告牌$AB$的高度.(结果保留一位小数.参考数据：$\sin39^{\circ}\approx0.63$,$\cos39^{\circ}\approx0.78$,$\tan39^{\circ}\approx0.81$,$\sqrt{3}\approx1.73$)

答案： 解:在Rt△BCD中,BC=DC·tan30°=15×$\frac{\sqrt{3}}{3}$=5$\sqrt{3}$(m),在Rt△ACD中,AC=DC·tan39°≈15×0.81=12.15(m),
∴AB=AC - BC≈12.15 - 5$\sqrt{3}$≈3.5(m).答:广告牌AB的高度约为3.5m.

3. 如图,某飞机于空中$A处探测到正下方的地面目标C$,此时飞机高度$AC为1400m$,从飞机上看地面控制点$B的俯角为\alpha$,则$B$,$C$之间的距离为(A)


A.$\dfrac{1400}{\tan\alpha}m$
B.$1400\tan\alpha m$
C.$1400\sin\alpha m$
D.$1400\cos\alpha m$

答案： A

4. (2023·湖北襄阳中考)在襄阳市诸葛亮广场上矗立着一尊诸葛亮铜像.某校数学兴趣小组利用热气球开展综合实践活动,测量诸葛亮铜像的高度.如图,在点$C$处,探测器显示,热气球到铜像底座底部所在水平面的距离$CE为32m$,从热气球$C看铜像顶部A的俯角为45^{\circ}$,看铜像底部$B的俯角为63.4^{\circ}$.已知底座$BD的高度为4m$,求铜像$AB$的高度.(结果保留整数.参考数据：$\sin63.4^{\circ}\approx0.89$,$\cos63.4^{\circ}\approx0.45$,$\tan63.4^{\circ}\approx2.00$,$\sqrt{2}\approx1.41$)

答案： 解:在矩形BDEF中,EF=BD=4,CE=32,
∴CF=32 - 4 = 28.
∵tan∠CBF=tan63.4°=$\frac{CF}{BF}$,
∴2≈$\frac{28}{BF}$,即BF≈14,
∴CG=BF≈14.
∵∠GCA=45°,
∴AG=GC≈14,
∴AB=BG - AG=CF - AG≈28 - 14 = 14(m).答:铜像AB的高度约为14m.

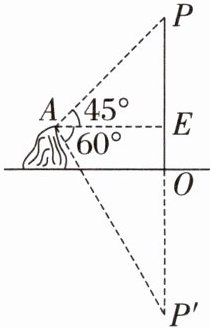
5. 如图,在湖边高出水面$50m的山顶A$处看见一艘飞艇停留在湖面上空某处,观察到飞艇底部标志$P处的仰角为45^{\circ}$,又观其在湖中之像的俯角为$60^{\circ}$,则飞艇底部$P$距离湖面的高度为(D)


A.$(25\sqrt{3}+75)m$
B.$(50\sqrt{3}+50)m$
C.$(75\sqrt{3}+75)m$
D.$(50\sqrt{3}+100)m$

答案： D[提示:设AE=xm,在Rt△AEP中,∠PAE=45°,则∠P=45°,
∴PE=AE=xm.
∵山顶A处高出水面50m,
∴OE=50m,
∴OP'=OP=PE + OE=(x + 50)m.
∵∠P'AE=60°,
∴P'E=tan60°·AE=$\sqrt{3}$xm,
∴OP'=P'E - OE=($\sqrt{3}$x - 50)m,
∴x + 50=$\sqrt{3}$x - 50,解得x=50($\sqrt{3}$+1).
∴PO=PE + OE=50($\sqrt{3}$+1)+50=(50$\sqrt{3}$+100)(m),即飞艇底部P距离湖面的高度是(50$\sqrt{3}$+100)m.]

6. (2023·临沂期中)如图,一架无人机在空中$A处测得某校旗杆顶部B的仰角为30^{\circ}$,底部$C的俯角为60^{\circ}$,无人机与旗杆的水平距离$AD为6m$,求该校的旗杆高为多少米.(结果保留根号)

答案： 解:在Rt△ABD中,
∵AD=6,∠BAD=30°,
∴tan30°=$\frac{BD}{AD}$=$\frac{BD}{6}$=$\frac{\sqrt{3}}{3}$,解得BD=2$\sqrt{3}$.在Rt△ACD中,
∵AD=6,∠CAD=60°,
∴tan60°=$\frac{CD}{AD}$=$\frac{CD}{6}$=$\sqrt{3}$,解得DC=6$\sqrt{3}$.故该校的旗杆高为BC=BD + DC=2$\sqrt{3}$+6$\sqrt{3}$=8$\sqrt{3}$(m).答:该校的旗杆高为8$\sqrt{3}$m.