《2025年全科王同步课时练习九年级数学上册青岛版》

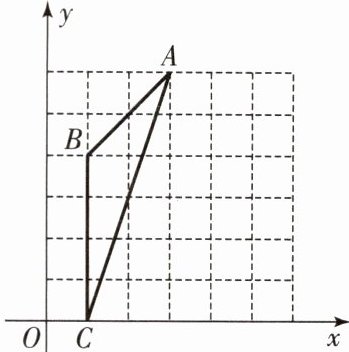
11. (素养题)如图,在平面直角坐标系 $ xOy $ 中,$ A(3,6) $,$ B(1,4) $,$ C(1,0) $,则 $ \triangle ABC $ 外接圆的圆心坐标是 ( )


A.$ (4,2) $
B.$ (4,3) $
C.$ (5,3) $
D.$ (5,2) $

答案：
D [提示:如图,圆心即为所求,
∴ 圆心的坐标为(5,2).]

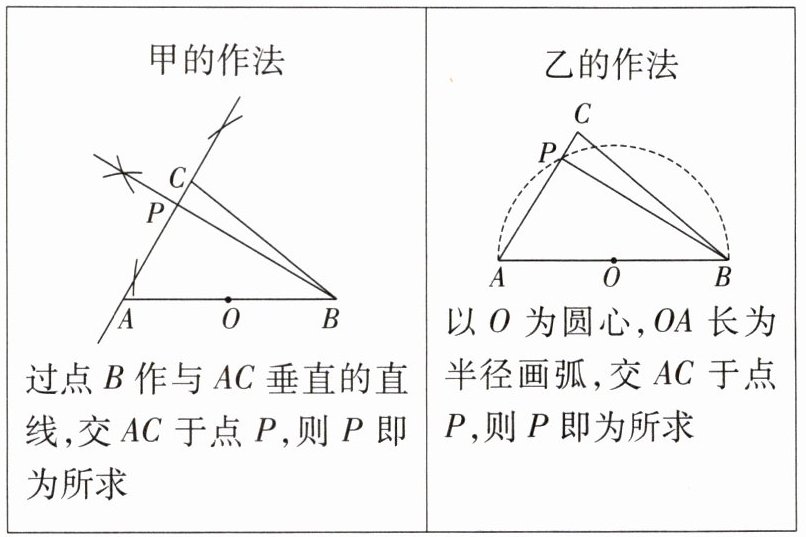
12. (新考法)如图,锐角三角形 $ ABC $ 中,点 $ O $ 为 $ AB $ 的中点. 甲、乙两人想在 $ AC $ 上找一点 $ P $,使得 $ \triangle ABP $ 的外心为点 $ O $,其作法分别如下. 对于甲、乙两人的作法,下列判断正确的是 (A)


A.两人都正确
B.两人都错误
C.甲正确,乙错误
D.甲错误,乙正确

答案： A [提示:甲的作法,
∵ BP⊥AC,
∴ ∠APB=90°.
∵ O 是 AB 的中点,
∴$PO=\frac{1}{2}$AB,
∴ PO=AO=BO,
∴ O 是△PAB 的外心,
∴ 甲的作法正确.乙的作法,由作法知,OA=OB=OP,
∴ O 是△PAB 的外心,
∴ 乙的作法正确.]

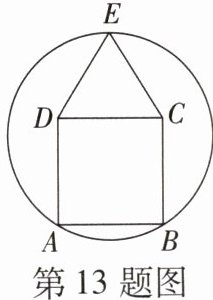
13. (2023·潍坊寒亭区期中)将边长相等的正方形和等边三角形如图放置,过 $ A,B,E $ 三点作圆,则劣弧 $ \overset{\frown}{AB} $ 所对的圆心角的度数是 ( )


A.$ 15^{\circ} $
B.$ 30^{\circ} $
C.$ 60^{\circ} $
D.$ 90^{\circ} $

答案：
C [提示:连接 EB,EA,
∵ ABCD 是正方形,△CDE 是等边三角形,
∴ EC=CD=CB,$∠DEC=∠ECD=60°$,$∠BCD=90°$,
∴$∠ECB=150°$,
∴$∠CEB=15°$,同理$∠AED=15°$,
∴$∠AEB=30°$,
∴ 劣弧$\overset{\frown}{AB}$所对的圆心角的度数是 60°.]

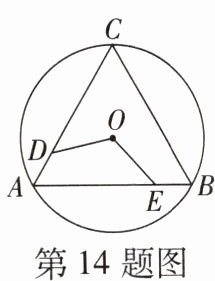
14. 如图,$ \triangle ABC $ 是 $ \odot O $ 的内接正三角形,点 $ O $ 是圆心,点 $ D,E $ 分别在边 $ AC,AB $ 上,若 $ DA = EB $,则 $ \angle DOE $ 的度数是______.

120°

答案： 120°[提示:连接 OA,OB,
∵ △ABC 是⊙O 的内接正三角形,
∴$∠AOB=120°$.
∵ OA=OB,
∴$∠OAB=∠OBA=30°$.
∵$∠CAB=60°$,
∴$∠OAD=30°$,
∴$∠OAD=∠OBE$.
∵ AD=BE,AO=BO,
∴ △OAD≌△OBE,
∴$∠DOA=∠BOE$,
∴$∠DOE=∠DOA+∠AOE=∠AOE+∠BOE=∠AOB=120°$.]

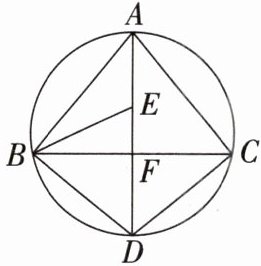
15. 如图,$ AD $ 为 $ \triangle ABC $ 外接圆的直径,$ AD \perp BC $,垂足为点 $ F $,$ \angle ABC $ 的平分线交 $ AD $ 于点 $ E $,连接 $ BD,CD $.
(1)求证：$ BD = CD $.
(2)已知 $ \angle BAD = \angle CBD $,请判断 $ B,E,C $ 三点是否在以 $ D $ 为圆心,以 $ DB $ 为半径的圆上,并说明理由.

答案：
(1)证明:
∵ AD 为直径,AD⊥BC,
∴$\overset{\frown}{BD}=\overset{\frown}{CD}$,
∴ BD=CD.
(2)解:B,E,C 三点在以 D 为圆心,以 DB 为半径的圆上.理由如下:
∵ BE 平分$∠ABC$,
∴$∠CBE=∠ABE$.
∵$∠DBE=∠CBD+∠CBE$,$∠DEB=∠BAD+∠ABE$,且$∠BAD=∠CBD$,
∴$∠DBE=∠DEB$,
∴ DB=DE.由
(1)知 BD=CD,
∴ DB=DE=DC,
∴ B,E,C 三点在以 D 为圆心,以 DB 为半径的圆上.

16. 如图,残破的圆形轮片上,弦 $ AB $ 的垂直平分线交 $ \overset{\frown}{AB} $ 于点 $ C $,交弦 $ AB $ 于点 $ D $. 已知 $ AB = 24\mathrm{cm} $,$ CD = 8\mathrm{cm} $.
(1)求作此残片所在的圆；(不写作法,保留作图痕迹)
(2)求(1)中所作圆的半径.

答案：
解:
(1)如图,作弦 AC 的垂直平分线与弦 AB 的垂直平分线交于 O 点,以 O 为圆心,OC 长为半径作圆 O 就是此残片所在的圆.
(2)如图,连接 OA,设 OA=x cm,
∵ CO 是半径,CO⊥AB,AB=24 cm,CD=8 cm,
∴ AD=12 cm,OD=(x-8)cm,根据勾股定理,得$x^{2}=12^{2}+(x-8)^{2}$,解得 x=13.
∴ 圆的半径为 13 cm.