《2025年全科王同步课时练习九年级数学上册青岛版》

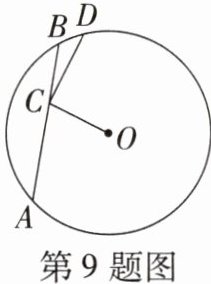
9. 如图,在$\odot O$中,弦$AB = 8$,点$C在线段AB$上移动,连接$OC$,过点$C作CD \perp OC交\odot O于点D$,则$CD$的最大值是(4)

A.$2$
B.$4$
C.$6$
D.$8$

答案： B[提示:如图,作OH⊥AB于H,连接OA,OD,
∴AH = BH = $\frac{1}{2}$AB = $\frac{1}{2}$×8 = 4.
∵CD⊥OC,
∴CD = $\sqrt{OD² - OC²}$.
∵OD为定值，当OC最小时，CD最大,
∴当OC = OH时,CD的值最大，
∴CD的最大值为4.]

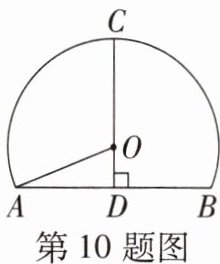
10. (素养题)如图是一个高速公路的隧道的横截面,它的形状是以$O$为圆心的圆的一部分,如果$D是\odot O中弦AB$的中点,$CD经过圆心O交\odot O于点C$,$AB = 24$,$CD = 18$,则此圆的半径$OA$的长为______.

13

答案： 13
∵点D是⊙O中弦AB的中点，CD经过圆心O交⊙O于点C,
∴CD⊥AB,
∴∠ADO = 90°.
∵AB = 24,
∴AD = $\frac{1}{2}$AB = 12.设圆的半径OA = r,则OD = 18 - r,在Rt△AOD中,AO² = AD² + OD²,即r² = (18 - r)² + 12²,解得r = 13.]

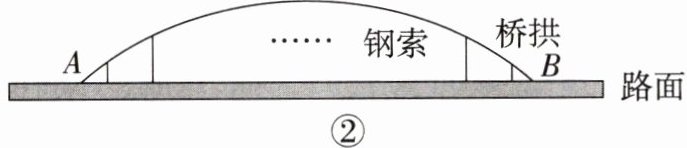
11. (2023·威海期中)如图①,武汉晴川桥可以近似地看作半径为$250\ m$的圆弧(示意图如图②),桥拱和路面之间用数根钢索垂直相连,其正下方的路面$AB长300\ m$,那么这些钢索中最长的一根长50$m$.
]

答案： 50[提示:设圆弧的圆心为O,过O作OC⊥AB于C,交⌒AB于D,连接OA,如图,则OA = OD = 250m,AC = BC = $\frac{1}{2}$AB = 150m,
∴OC = $\sqrt{OA² - AC²}$ = $\sqrt{250² - 150²}$ = 200(m),
∴CD = OD - OC = 250 - 200 = 50(m),即这些钢索中最长的一根为50m.]

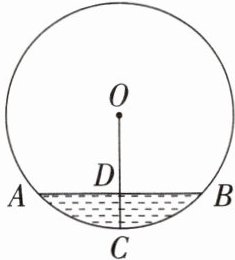
12. (2023·青岛市南区校级月考)如图是一个管道的横截面,圆心$O到水面AB的距离OD是3$,水面宽$AB = 6$.
(1)求这个管道横截面的半径；
(2)求$\angle AOB$的度数.
]

答案： 解:
(1)连接OA,
∵AB = 6,OD⊥AB,
∴AD = 3.
∵OD = 3,
∴△OAD是等腰直角三角形.在Rt△AOD中，AO = $\sqrt{AD² + OD²}$ = $\sqrt{3² + 3²}$ = 3√2,
∴这个管道横截面的半径为3√2.　　
(2)连接OB,由
(1)知在等腰直角三角形ADO中，∠AOD = 45°，在等腰直角三角形BDO中，∠BOD = 45°,
∴∠AOB = ∠AOD + ∠BOD = 45° + 45° = 90°.

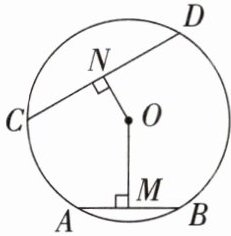
13. 如图,$AB和CD分别是\odot O$的两条弦,过点$O分别作ON \perp CD于点N$,$OM \perp AB于点M$,若$ON = \dfrac{1}{2}AB$,求证：$OM = \dfrac{1}{2}CD$.
]

答案： 证明:如图,连接OA,OC,设圆的半径是r,ON = x,则AB = 2x.在Rt△CON中,CN² = OC² - ON² = r² - x².
∵ON⊥CD,
∴CD = 2CN = 2$\sqrt{r² - x²}$.
∵OM⊥AB,
∴AM = $\frac{1}{2}$AB = x.在Rt△AOM中,OM = $\sqrt{OA² - AM²}$ = $\sqrt{r² - x²}$,
∴OM = $\frac{1}{2}$CD.

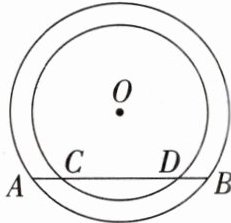
14. 如图,在以点$O$为圆心的两个同心圆中,大圆的弦$AB交小圆于点C$,$D$.
(1)求证：$AC = BD$；
(2)若大圆的半径$R = 10$,小圆的半径$r = 8$,且点$O到直线AB的距离为6$,求$AC$的长.
]

答案：
(1)证明:如图,过O作OE⊥AB于点E,则CE = DE,AE = BE,
∴BE - DE = AE - CE,即AC = BD.　　
(2)解:由
(1)可知OE⊥AB,如图,连接OC,OA,
∴OE = 6,CE = $\sqrt{OC² - OE²}$ = $\sqrt{8² - 6²}$ = 2√7,AE = $\sqrt{OA² - OE²}$ = $\sqrt{10² - 6²}$ = 8,
∴AC = AE - CE = 8 - 2√7.

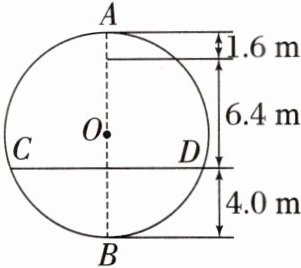
15. 如图所示的是一张盾构隧道断面结构图. 隧道内部为以$O$为圆心,$AB$为直径的圆. 隧道内部共分为三层,上层为排烟道,中间为行车隧道,下层为服务层. 点$A到顶棚的距离为1.6\ m$,顶棚到路面的距离是$6.4\ m$,点$B到路面的距离为4.0\ m$. 请求出路面$CD$的宽度.(结果精确到$0.1\ m$. 参考数据：$\sqrt{2} \approx 1.41$)
]

答案： 解:如图,连接OC,设AB交CD于E,由题意知AB = 1.6 + 6.4 + 4 = 12,
∴OC = OB = 6,
∴OE = OB - BE = 6 - 4 = 2.由题意可知AB⊥CD.
∵AB过点O,
∴CD = 2CE.在Rt△OCE中,由勾股定理,得CE = $\sqrt{OC² - OE²}$ = $\sqrt{6² - 2²}$ = 4√2,
∴CD = 2CE = 8√2≈11.3(m).
∴路面CD的宽度约为11.3m.