第10页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
9. 如图,每个小正方形的边长均为1,则下列图中的三角形(阴影部分)与图中$\triangle ABC$相似的是(
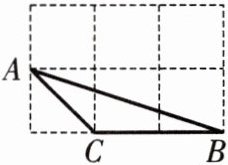
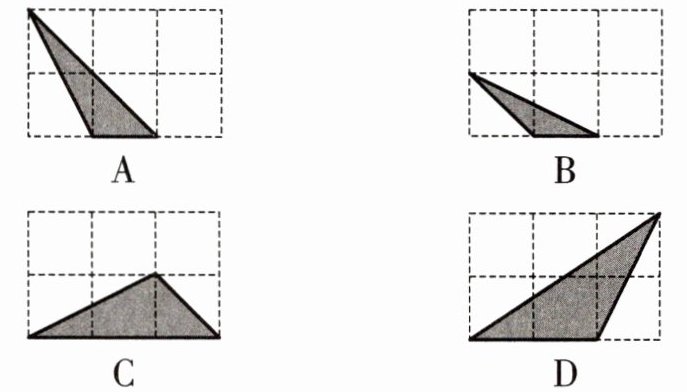
B
)

答案:
B
10. 如图,在由小正方形组成的网格上有6个三角形:①$\triangle ABC$,②$\triangle CDB$,③$\triangle DEB$,④$\triangle FBG$,⑤$\triangle HGF$,⑥$\triangle EKF$. 在三角形②~⑥中,与①相似的三角形的序号是______.
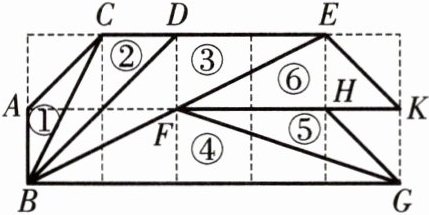

答案:
③④⑤[提示:设每个小正方形的边长都为1,则△ABC的各边长分别为1,√2,√5;②△BCD的各边长分别为1,√5,2√2;③△BDE的各边长分别为2,2√2,2√5(为△ABC对应各边长的2倍);④△BFG的各边长分别为√5,√10,5(为△ABC对应各边长的√5倍);⑤△FGH的各边长分别为√2,2,√10(为△ABC对应各边长的√2倍);⑥△EFK的各边长分别为3,√2,√5.根据三组对应边的比相等的两个三角形相似得到与三角形①相似的是③④⑤.]
11. 如图,$AD$,$A'D'分别是\triangle ABC和\triangle A'B'C'$的中线,且$\frac{AB}{A'B'}= \frac{BD}{B'D'}= \frac{AD}{A'D'}$,判断$\triangle ABC和\triangle A'B'C'$是否相似,并说明理由.
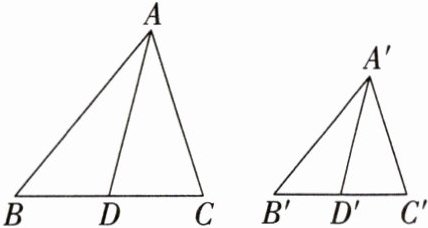

答案:
解:△ABC∽△A'B'C',理由如下:
∵AB/A'B'=BD/B'D'=AD/A'D',
∴△ABD∽△A'B'D',
∴∠B=∠B'.
∵AD,A'D'分别是△ABC和△A'B'C'的中线,
∴BD=1/2BC,B'D'=1/2B'C',
∴AB/A'B'=(1/2BC)/(1/2B'C')=BC/B'C'.在△ABC和△A'B'C'中,
∵AB/A'B'=BC/B'C',∠B=∠B',
∴△ABC∽△A'B'C'.
∵AB/A'B'=BD/B'D'=AD/A'D',
∴△ABD∽△A'B'D',
∴∠B=∠B'.
∵AD,A'D'分别是△ABC和△A'B'C'的中线,
∴BD=1/2BC,B'D'=1/2B'C',
∴AB/A'B'=(1/2BC)/(1/2B'C')=BC/B'C'.在△ABC和△A'B'C'中,
∵AB/A'B'=BC/B'C',∠B=∠B',
∴△ABC∽△A'B'C'.
12. 如图,在四边形$ABCD$中,$AC$,$BD相交于点F$,点$E在BD$上,且$\frac{AB}{AE}= \frac{BC}{ED}= \frac{AC}{AD}$.
(1)$\angle BAE与\angle CAD$相等吗?为什么?
(2)试判断$\triangle ABE与\triangle ACD$是否相似,并说明理由.
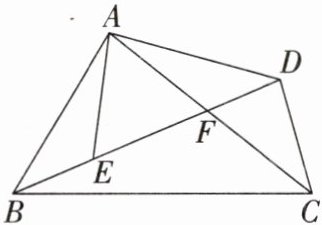
(1)$\angle BAE与\angle CAD$相等吗?为什么?
(2)试判断$\triangle ABE与\triangle ACD$是否相似,并说明理由.

答案:
解:
(1)∠BAE与∠CAD相等.理由如下:
∵AB/AE=BC/DE=AC/AD,
∴△ABC∽△AED,
∴∠BAC=∠EAD,
∴∠BAC - ∠EAF=∠EAD - ∠EAF,
∴∠BAE=∠CAD.
(2)△ABE与△ACD相似.理由如下:
∵AB/AE=AC/AD,
∴AB/AC=AE/AD.在△ABE与△ACD中,
∵AB/AC=AE/AD,∠BAE=∠CAD,
∴△ABE∽△ACD.
(1)∠BAE与∠CAD相等.理由如下:
∵AB/AE=BC/DE=AC/AD,
∴△ABC∽△AED,
∴∠BAC=∠EAD,
∴∠BAC - ∠EAF=∠EAD - ∠EAF,
∴∠BAE=∠CAD.
(2)△ABE与△ACD相似.理由如下:
∵AB/AE=AC/AD,
∴AB/AC=AE/AD.在△ABE与△ACD中,
∵AB/AC=AE/AD,∠BAE=∠CAD,
∴△ABE∽△ACD.
13. 如图,在$\triangle ABC和\triangle A'B'C'$中,$D$,$D'分别是AB$,$A'B'$上一点,$\frac{AD}{AB}= \frac{A'D'}{A'B'}$.
(1)当$\frac{CD}{C'D'}= \frac{AC}{A'C'}= \frac{AB}{A'B'}$时,求证:$\triangle ABC\backsim\triangle A'B'C'$. 证明的思路可以用下面的框图表示,请填写其中的空格.
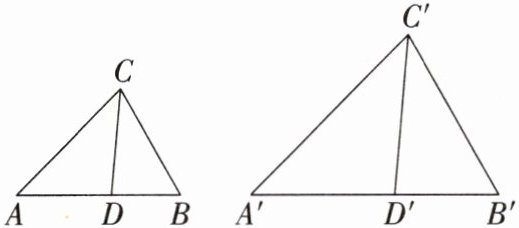
(2)当$\frac{CD}{C'D'}= \frac{AC}{A'C'}= \frac{BC}{B'C'}$时,判断$\triangle ABC与\triangle A'B'C'$是否相似,并说明理由.

(1)当$\frac{CD}{C'D'}= \frac{AC}{A'C'}= \frac{AB}{A'B'}$时,求证:$\triangle ABC\backsim\triangle A'B'C'$. 证明的思路可以用下面的框图表示,请填写其中的空格.

(2)当$\frac{CD}{C'D'}= \frac{AC}{A'C'}= \frac{BC}{B'C'}$时,判断$\triangle ABC与\triangle A'B'C'$是否相似,并说明理由.

答案:
解:
(1)CD/C'D'=AC/A'C'=AD/A'D' ∠A=∠A'
(2)相似.理由如下:如图,过点D,D'分别作DE//BC,D'E'//B'C',DE交AC于E,D'E'交A'C'于E'.
∵DE//BC,
∴△ADE∽△ABC,
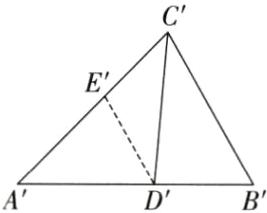
∴AD/AB=DE/BC=AE/AC.同理A'D'/A'B'=D'E'/B'C'=A'E'/A'C'.
∵AD/AB=A'D'/A'B',
∴DE/BC=D'E'/B'C',
∴DE/D'E'=BC/B'C'.同理,AE/AC=A'E'/A'C'.
∴(AC - AE)/AC=(A'C' - A'E')/A'C',即EC/AC=E'C'/A'C',
∴EC/E'C'=AC/A'C'.
∵CD/C'D'=AC/A'C'=BC/B'C',
∴CD/C'D'=DE/D'E'=EC/E'C',
∴△DCE∽△D'C'E',
∴∠CED=∠C'E'D'.
∵DE//BC,
∴∠CED+∠ACB=180°.同理,∠C'E'D'+∠A'C'B'=180°,
∴∠ACB=∠A'C'B'.
∵AC/A'C'=CB/C'B',
∴△ABC∽△A'B'C'.
解:
(1)CD/C'D'=AC/A'C'=AD/A'D' ∠A=∠A'
(2)相似.理由如下:如图,过点D,D'分别作DE//BC,D'E'//B'C',DE交AC于E,D'E'交A'C'于E'.
∵DE//BC,
∴△ADE∽△ABC,


∴AD/AB=DE/BC=AE/AC.同理A'D'/A'B'=D'E'/B'C'=A'E'/A'C'.
∵AD/AB=A'D'/A'B',
∴DE/BC=D'E'/B'C',
∴DE/D'E'=BC/B'C'.同理,AE/AC=A'E'/A'C'.
∴(AC - AE)/AC=(A'C' - A'E')/A'C',即EC/AC=E'C'/A'C',
∴EC/E'C'=AC/A'C'.
∵CD/C'D'=AC/A'C'=BC/B'C',
∴CD/C'D'=DE/D'E'=EC/E'C',
∴△DCE∽△D'C'E',
∴∠CED=∠C'E'D'.
∵DE//BC,
∴∠CED+∠ACB=180°.同理,∠C'E'D'+∠A'C'B'=180°,
∴∠ACB=∠A'C'B'.
∵AC/A'C'=CB/C'B',
∴△ABC∽△A'B'C'.
查看更多完整答案,请扫码查看


