第83页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. 如图,已知$\odot O$的半径为6,$AB$,$BC是\odot O$的弦,若$\angle ABC = 60°$,则劣弧$\overset{\frown}{AC}$的长是(
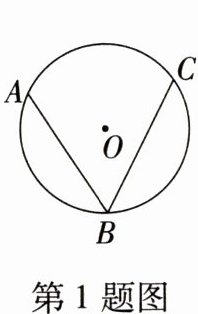
A.$3\pi$
B.$4\pi$
C.$10\pi$
D.$12\pi$
B
)
A.$3\pi$
B.$4\pi$
C.$10\pi$
D.$12\pi$
答案:
B
2. (2023·辽宁朝阳中考)如图,四边形$ABCD内接于\odot O$,若$\angle C = 120°$,$\odot O$的半径为3,则劣弧$\overset{\frown}{BD}$的长为(

A.$\pi$
B.$2\pi$
C.$3\pi$
D.$6\pi$
B
)
A.$\pi$
B.$2\pi$
C.$3\pi$
D.$6\pi$
答案:
B
3. 如图,$AB是半圆O$的直径,$C是半圆O$上一点,连接$AC$,$BC$,若半圆$O$的半径为5,$\angle B = 58°$,则$\overset{\frown}{BC}$的长为(
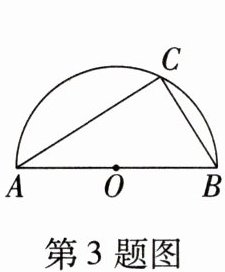
A.$\frac{4}{5}\pi$
B.$\frac{8}{5}\pi$
C.$\frac{16}{5}\pi$
D.$\frac{16}{9}\pi$
D
)
A.$\frac{4}{5}\pi$
B.$\frac{8}{5}\pi$
C.$\frac{16}{5}\pi$
D.$\frac{16}{9}\pi$
答案:
D
4. 如图,扇形$OAB的圆心角是90°$,半径$OA$为1,则$\overset{\frown}{AB}$的长是
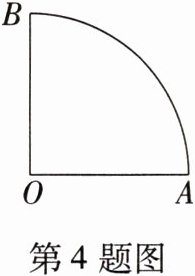
$\frac{1}{2}\pi$
.(结果保留$\pi$)
答案:
$\frac{1}{2}\pi$
5. 如图,$\overset{\frown}{AB}的半径OA = 2$,$OC \perp AB于点C$,$\angle AOC = 60°$,求$\overset{\frown}{AB}$的长.


答案:
解:
∵ $OC \perp AB$, $\angle AOC = 60°$,
∴ $\angle AOB = 120°$.
∵ $OA = 2$,
∴ $\overset{\frown}{AB}$的长是$\frac{120\pi × 2}{180} = \frac{4\pi}{3}$.
∵ $OC \perp AB$, $\angle AOC = 60°$,
∴ $\angle AOB = 120°$.
∵ $OA = 2$,
∴ $\overset{\frown}{AB}$的长是$\frac{120\pi × 2}{180} = \frac{4\pi}{3}$.
6. 如图,在$Rt\triangle ABC$中,$\angle B = 90°$,$AB = 6$,$AC = 10$,以边$BC$为直径作一个半圆,则半圆(阴影部分)的面积为(
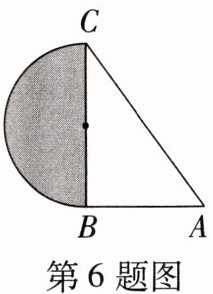
A.$4\pi$
B.$8\pi$
C.$12\pi$
D.$16\pi$
B
)
A.$4\pi$
B.$8\pi$
C.$12\pi$
D.$16\pi$
答案:
B
7. 如图①是一块弘扬“社会主义核心价值观”的扇面宣传展板,该展板的部分示意图如图②,它是以$O$为圆心,$OA$,$OB$长分别为半径,圆心角$\angle O = 120°$形成的扇面,若$OA = 4m$,$OB = 2m$,则阴影部分的面积是(

A.$\frac{4}{3}\pi m^2$
B.$\frac{8}{3}\pi m^2$
C.$4\pi m^2$
D.$\frac{16}{3}\pi m^2$
C
)
A.$\frac{4}{3}\pi m^2$
B.$\frac{8}{3}\pi m^2$
C.$4\pi m^2$
D.$\frac{16}{3}\pi m^2$
答案:
C[提示:$S_{阴影}=S_{扇形AOD}-S_{扇形BOC}=\frac{120\pi \cdot OA^2}{360}-\frac{120\pi \cdot OB^2}{360}=\frac{120\pi(OA^2 - OB^2)}{360}=\frac{\pi(4^2 - 2^2)}{3}=4\pi(m^2)$.]
8. 如图,边长为2的正方形$ABCD$的中心与半径为2的$\odot O$的圆心重合,$E$,$F分别是AD$,$BA的延长线与\odot O$的交点,则图中阴影部分的面积是

$\pi - 1$
.(结果保留$\pi$)
答案:
$\pi - 1$[提示:如图,延长 $DC$, $CB$ 交$\odot O$于$J$, $K$. 则$\odot O$被分成5个部分,其中4个部分是全等图形,
∴ 图中阴影部分的面积$=\frac{1}{4}(4\pi - 4)=\pi - 1$.]
∴ 图中阴影部分的面积$=\frac{1}{4}(4\pi - 4)=\pi - 1$.]
9. 如图是一个半圆,已知$AB = 10cm$,阴影部分的面积是$24.25cm^2$,求图中三角形$AB$边上的高.($\pi取3.14$)
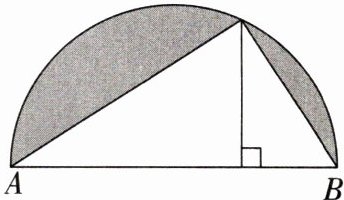

答案:
解:设图中三角形 $AB$ 边上的高为$h$,
∵ $AB = 10\ cm$, 阴影部分的面积是$24.25\ cm^2$,
∴ $\frac{\pi \cdot (\frac{10}{2})^2}{2}-\frac{1}{2} × 10h = 24.25$,解得$h = 3$,
∴ 图中三角形 $AB$ 边上的高为$3\ cm$.
∵ $AB = 10\ cm$, 阴影部分的面积是$24.25\ cm^2$,
∴ $\frac{\pi \cdot (\frac{10}{2})^2}{2}-\frac{1}{2} × 10h = 24.25$,解得$h = 3$,
∴ 图中三角形 $AB$ 边上的高为$3\ cm$.
查看更多完整答案,请扫码查看


