《2025年全科王同步课时练习九年级数学上册青岛版》

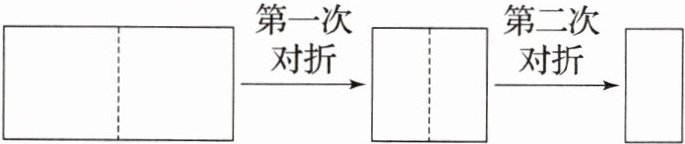
11. 如图,取一张长为a,宽为b的长方形纸片,将它对折两次后得到一张小长方形纸片,若要使小长方形与原长方形相似,则原长方形纸片的边a,b应满足的条件是(B)

A.$a = \sqrt{2}b$
B.$a = 2b$
C.$a = 2\sqrt{2}b$
D.$a = 4b$

答案： B[提示：对折两次后的小长方形的长为b，宽为$\frac{1}{4}$a。
∵小长方形与原长方形相似，
∴$\frac{a}{b}=\frac{b}{\frac{1}{4}a}$，
∴$a = 2b$。]

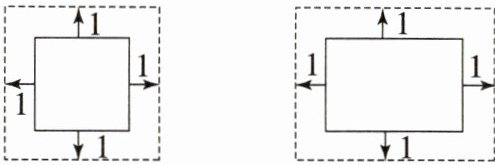
12. 边长为4的正方形和长、宽分别为6,4的矩形按如图所示的方式向外扩张,各得到一个新图形,它们的对应边间距均为1,则新图形与原图形相似的有______个.

答案：
1[提示：如图
(1)，
∵正方形的边长由4变为6，对应边比值相等，对应角相等，故新图形与原图形相似。如图
(2)，
∵AB = CD = 4，AD = BC = 6，则A'B' = C'D' = 4 + 2 = 6，A'D’ = B'C' = 6 + 2 = 8，则得$\frac{AB}{A'B'}\neq\frac{BC}{B'C'}$，
∴新矩形与原矩形不相似。]

13. 如图,在梯形ABCD中,AD//BC,E,F两点分别在AB,DC上. 若AE = 4,EB = 6,DF = 2,FC = 3,且梯形AEFD与梯形EBCF相似,则AD与BC的长度比为4:9.

答案： 4:9[提示：
∵梯形AEFD∽梯形EBCF，且DF:FC = 2:3，
∴AD:EF = EF:BC = 2:3，
∴$AD=\frac{2}{3}EF$，$BC=\frac{3}{2}EF$，
∴$AD:EF:BC=\frac{2}{3}:1:\frac{3}{2}=4:6:9$，
∴AD:BC = 4:9。]

14. 如图,一个矩形广场的长为100 m,宽为80 m,广场外围两条纵向小路的宽均为1.5 m,如果设两条横向小路的宽都为x(x ＜ 1.5)m,那么当x为多少时,小路内、外边缘所围成的两个矩形相似？

答案： 解：要使小路内、外边缘所围成的两个矩形相似，则有(100 + 2x):100 = (80 + 2x):80，解得x = 1.2。
∴当x为1.2时，小路内、外边缘所围成的两个矩形相似。

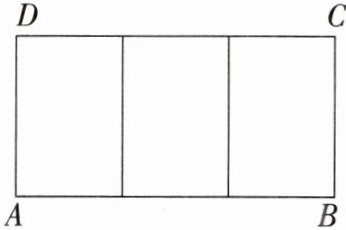
15. (易错题)如图,一个矩形的长AB = a m,宽AD = 1 m,按照图中所示的方式将它分割成相同的三个矩形,且每个小矩形与原矩形相似,求a的值.

答案： 解：
∵每个小矩形与原矩形相似，
∴$\frac{1}{a}=\frac{a}{3}$，解得$a = \sqrt{3}$或$a = -\sqrt{3}$(舍去)，
∴$a = \sqrt{3}$。

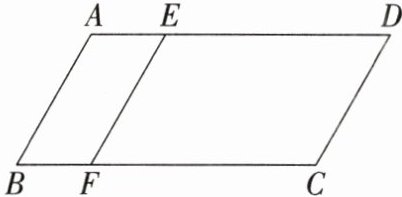
16. 如图,在▱ABCD中,AB//EF,若AB = 1,AD = 2,AE = $\frac{1}{2}$AB,则▱ABFE与▱BCDA相似吗？说明理由.

答案： 解：相似。理由如下：
∵AB = 1，AD = 2，$AE=\frac{1}{2}AB$，
∴$\frac{AE}{AB}=\frac{AB}{AD}=\frac{1}{2}$。
∵四边形ABCD是平行四边形，AB//EF，
∴∠A = ∠C = ∠BFE，∠B = ∠D = ∠AEF。
∴▱ABFE与▱BCDA相似。

17. 矩形ABCD的长AB = 30,宽BC = 20.
(1) 如图①,若沿矩形ABCD四周有宽为1的环形区域,图中所形成的两个矩形ABCD与A'B'C'D'相似吗？请说明理由.
(2) 如图②,当x为多少时,矩形ABCD与矩形A'B'C'D'相似？

答案： 解：
(1)不相似，理由如下：
∵AB = 30，A'B' = 28，BC = 20，B'C' = 18，$\frac{28}{30}\neq\frac{18}{20}$，
∴不相似。
(2)由题意，得$\frac{30 - 2x}{30}=\frac{20 - 2}{20}$或$\frac{30 - 2x}{20}=\frac{20 - 2}{30}$，解得x = 1.5或x = 9。
∴当x = 1.5或x = 9时，矩形ABCD与矩形A'B'C'D'相似。