《2025年全科王同步课时练习九年级数学上册青岛版》

11. (2023·济宁邹城市期中)在平面直角坐标系$xOy$中,以点$(-3,4)$为圆心,4为半径的圆(C)
A.与$x$轴相交,与$y$轴相切
B.与$x$轴相离,与$y$轴相交
C.与$x$轴相切,与$y$轴相交
D.与$x$轴相切,与$y$轴相离

答案： C

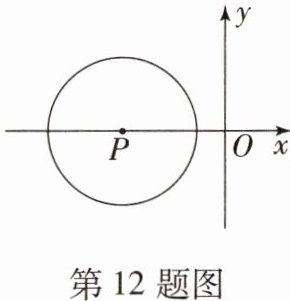
12. 如图,在平面直角坐标系中,半径为2的$\odot P的圆心P的坐标为(-3,0)$,将$\odot P沿x$轴正方向平移,使$\odot P与y$轴相交,则平移的距离$d$的取值范围是1＜d＜5.

答案： 1＜d＜5[提示:当⊙P位于y轴的左侧且与y轴相切时,平移的距离为1;当⊙P位于y轴的右侧且与y轴相切时,平移的距离为5.故平移的距离d的取值范围是1＜d＜5.]

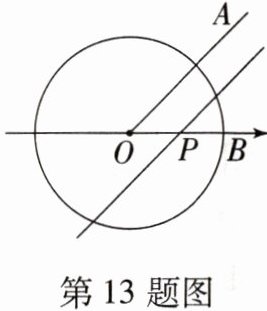
13. 如图,已知$\odot O是以数轴的原点O$为圆心,半径为1的圆,$\angle AOB = 45^{\circ}$,点$P$在数轴上运动,若过点$P且与OA平行的直线与\odot O$有公共点,设$OP = x$,则$x$的取值范围是0＜x≤$\sqrt{2}$.

答案： 0＜x≤$\sqrt{2}$

14. (2023·江苏镇江中考)已知一次函数$y = kx + 2$的图象经过第一、二、四象限,以坐标原点$O$为圆心,$r为半径作\odot O$.若对于符合条件的任意实数$k$,一次函数$y = kx + 2的图象与\odot O$总有两个公共点,则$r$的最小值为2.

答案： 2[提示:在y=kx+2中,令x=0,则y=2,
∴一次函数y=kx+2的图象与y轴交于(0,2),
∴一次函数的图象过定点(0,2).当⊙O过(0,2)时,两者至少有一个交点,
∵一次函数的图象经过第一、二、四象限,
∴直线与圆必有两个交点.而当⊙O半径小于2时,圆与直线存在相离的可能,
∴半径至少为2,故r的最小值为2.]

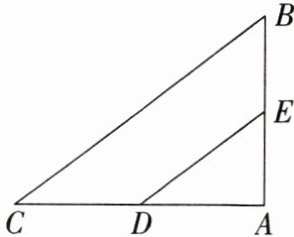
15. 如图,在$\triangle ABC$中,$AB = 3$,$AC = 4$,$BC = 5$,$D$,$E分别是AC$,$AB$的中点,试判定以$DE为直径的圆与BC$的位置关系.
]

答案： 解:过点A作AM⊥BC于点M,交DE于点N,
∵$3^2+4^2=5^2$,
∴△ABC是直角三角形,∠BAC=90°.
∴$S_{\triangle ABC}=\frac{1}{2}× AM× BC=\frac{1}{2}× AC× AB$,
∴AM=$\frac{3×4}{5}=2.4$.
∵D,E分别是AC,AB的中点,
∴DE//BC,DE=$\frac{1}{2}$BC=2.5.
∴AN=MN=$\frac{1}{2}$AM,
∴MN=1.2.
∵以DE为直径的圆半径为1.25,
∴r=1.25＞1.2.
∴以DE为直径的圆与BC的位置关系是相交.

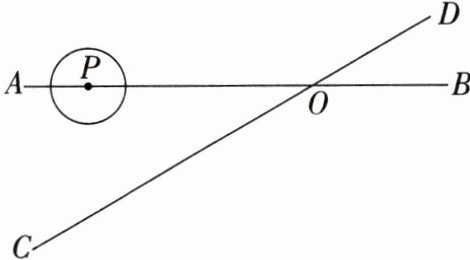
16. 如图,直线$AB$,$CD相交于点O$,$\angle AOC = 30^{\circ}$,半径为$1\mathrm{cm}的\odot P的圆心在直线OA$上,开始时,$PO = 6\mathrm{cm}$,如果$\odot P以1\mathrm{cm/s}的速度沿由A向B$的方向移动,那么当$\odot P的运动时间t$(单位：$\mathrm{s}$)满足什么条件时,$\odot P与直线CD$相切？
]

答案：
解:如图,当∠AOC=30°,半径为1 cm的⊙P'与直线CD相切时,P'E=1 cm,则OP'=2 cm,故PP'=4 cm,则当⊙P的运动时间为4 s时,⊙P与直线CD相切.当∠DOB=30°,半径为1 cm的⊙P''与直线CD相切时,P''F=1 cm,则OP''=2 cm,故PP''=8 cm,故当⊙P的运动时间为8 s时,⊙P与直线CD相切.综上所述,当⊙P的运动时间为4 s或8 s时,⊙P与直线CD相切.

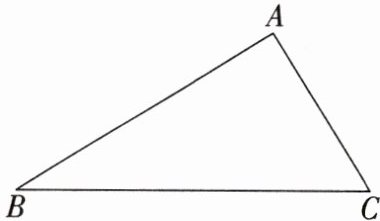
17. 如图,在$\mathrm{Rt}\triangle ABC$中,$\angle BAC = 90^{\circ}$.
(1) 先作$\angle ACB的平分线交AB边于点P$,再以点$P$为圆心,$PA长为半径作\odot P$；(要求：尺规作图,保留作图痕迹,不写作法)
(2) 请你判断(1)中$BC与\odot P$的位置关系,并证明你的结论.
]

答案：
解:
(1)如图,射线CP及⊙P为所求.
(2)BC与⊙P相切,理由如下:如图,过P作PD⊥BC,交BC于点D,
∵CP为∠ACB的平分线,且PA⊥AC,PD⊥CB,
∴PD=PA.
∵PA为⊙P的半径,
∴BC与⊙P相切.