《2025年全科王同步课时练习九年级数学上册青岛版》

7. (2023·聊城阳谷区模拟)如图,某商场准备将自动扶梯改造成斜坡式.已知商场的层高AB为6m,$ \angle ACB $为45°,改造后扶梯AD的坡比是$ 1:2 $,则改造后扶梯AD相比改造前AC增加的长度是(D)


A.6m
B.$ (12 - 6\sqrt{2})m $
C.$ (6\sqrt{2} - 4\sqrt{3})m $
D.$ (6\sqrt{5} - 6\sqrt{2})m $

答案： D[提示:在Rt△ABC中，∠ACB = 45°，AB = 6，sin45° = AB/AC = 6/AC = √2/2，解得AC = 6√2。
∵改造后扶梯AD的坡比是1:2，
∴AB/BD = 6/BD = 1/2，解得BD = 12，
∴AD = √(AB² + BD²)=6√5。
∴AD - AC = (6√5 - 6√2)m。]

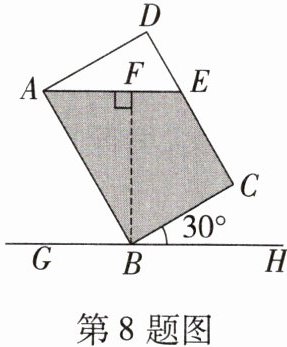
8. (2023·临沂郯城县期末)如图,矩形ABCD为一个正在倒水的水杯的截面图,$ AB = 18cm $,杯中水面与CD的交点为E,当水杯底面BC与水平面的夹角为30°时,杯中水的最大深度BF为(D)

A.9cm
B.15cm
C.$ 6\sqrt{3}cm $
D.$ 9\sqrt{3}cm $

答案： D[提示:过点A作AG⊥BH，垂足为G。如图，
∵四边形ABCD为矩形，
∴∠ABC = 90°。
∵∠CBH = 30°，
∴∠ABG = 180° - ∠ABC - ∠CBH = 60°。在Rt△AGB中，
∵sin∠ABG = AG/AB，
∴AG = AB·sin∠ABG = 18·sin60° = 18×√3/2 = 9√3(cm)。]

9. 小明坐于堤边垂钓,如图,河堤AC的坡角为30°,AC的长为$ \frac{3\sqrt{3}}{2} $米,钓竿OA的倾斜角α是60°,其长为3米,若OA与钓鱼线OB(假设钓鱼线是直的)的夹角为60°,则浮漂B与河堤下端C之间的距离是3/2米.
]

答案： 3/2米[提示:延长OA交BC的延长线于点D。
∵AO的倾斜角是60°，
∴∠ODB = 60°。
∵∠ACD = 30°，
∴∠CAD = 180° - ∠ODB - ∠ACD = 90°。在Rt△ACD中，AD = AC·tan∠ACD = 3√3/2×√3/3 = 3/2(米)，
∴CD = 2AD = 3米。又
∵∠O = 60°，
∴△BOD是等边三角形。
∴BD = OD = OA + AD = 3 + 3/2 = 9/2(米)，
∴BC = BD - CD = 9/2 - 3 = 3/2(米)。
∴浮漂B与河堤下端C之间的距离为3/2米。]

10. 为做好防汛工作,防汛指挥部决定对某水库的水坝进行加高加固,专家提供的方案是：水坝加高2米(即$ CD = 2 $米),背水坡DE的坡度$ i = 1:1 $(即$ DB:EB = 1:1 $),如图,已知$ AE = 4 $米,$ \angle EAC = 130^{\circ} $,求水坝原来的高度BC. (参考数据：$ \sin 50^{\circ}\approx 0.77 $,$ \cos 50^{\circ}\approx 0.64 $,$ \tan 50^{\circ}\approx 1.2 $)
]

答案： 解:设BC = x米，在Rt△ABC中，
∵∠CAB = 180° - ∠EAC = 50°，
∴AB = BC/tan50°≈BC/1.2 = 5/6x米。在Rt△EBD中，
∵DB:EB = 1:1，
∴BD = BE，
∴CD + BC = AE + AB，即2 + x = 4 + 5/6x，解得x = 12，即BC = 12米。
∴水坝原来的高度约为12米。

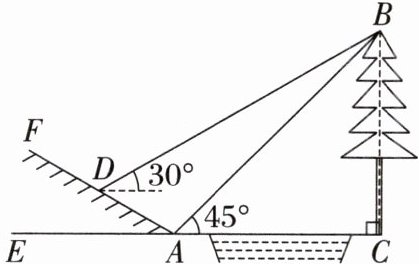
11. 如图,某数学活动小组想要测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是45°,坡角$ \angle FAE = 30^{\circ} $,求大树的高度. (结果保留根号)
]

答案： 解:如图，过点D作DG⊥BC于G，DH⊥CE于H，则四边形DHCG为矩形，
∴DG = CH，CG = DH。在Rt△AHD中，
∵∠DAH = 30°，AD = 6米，
∴DH = 3米，AH = 3√3米，
∴CG = 3米。设BC为x米，在Rt△ABC中，AC = BC/tan∠BAC = x米，
∴DG = (3√3 + x)米，BG = (x - 3)米。在Rt△BDG中，
∵BG = DG·tan30°，
∴x - 3 = (3√3 + x)×√3/3，解得x = 9 + 3√3，
∴BC = (9 + 3√3)米。
∴大树的高度为(9 + 3√3)米。

12. 某地的一座人行天桥如图,天桥高为6米,坡面BC的坡度为$ 1:1 $,文化墙PM在天桥底部正前方8米处(即$ PB = 8 $米),为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为$ 1:\sqrt{3} $. (参考数据：$ \sqrt{2}\approx 1.414 $,$ \sqrt{3}\approx 1.732 $)
(1) 若新坡面坡角为α,求坡角α的度数.
(2) 有关部门规定,文化墙距天桥底部小于3米时应拆除,天桥改造后,文化墙PM是否需要拆除？请说明理由.
]

答案： 解:
(1)
∵新坡面坡角为α，新坡面的坡度为1:√3，
∴tanα = 1/√3 = √3/3，
∴α = 30°。
(2)文化墙PM不需要拆除，理由如下:过C作CD⊥AB于点D，则CD = 6米，
∵新坡面的坡度为1:√3，
∴tan∠CAD = CD/AD = 6/AD = 1/√3，解得AD = 6√3米。
∵坡面BC的坡度为1:1，CD = 6米，
∴BD = 6米，
∴AB = AD - BD = (6√3 - 6)米。又
∵PB = 8米，
∴PA = PB - AB = 8 - (6√3 - 6) = 14 - 6√3≈14 - 6×1.732≈3.6(米)，3.6 ＞ 3，
∴文化墙PM不需要拆除。