《2025年全科王同步课时练习九年级数学上册青岛版》

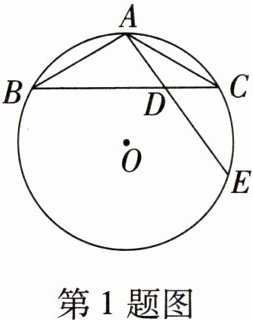
1. (2023·山东淄博中考)如图,△ABC是⊙O的内接三角形,AB= AC,∠BAC= 120°,D是BC边上一点,连接AD并延长交⊙O于点E.若AD= 2,DE= 3,则⊙O的半径为(√10)

A.√{10}
B.$\dfrac{3}{2}\sqrt{10}$
C.2√{10}
D.3√{10}

答案： 1.A [提示:如图,连接OA,OC,CE,
∵AB=AC,∠BAC=120°,
∴∠B=∠ACB=30°,
∴∠AOC=60°.
∵OA=OC,
∴△AOC是等边三角形,
∴AC=OA.
∵∠AEC=∠ACB=30°,∠CAD=∠EAC,
∴△ACD∽△AEC,
∴AC/AD=AE/AC,
∴AC²=AD·AE.
∵AD=2,DE=3,
∴AC=√(AD·AE)=√(2×(2+3))=√10,
∴OA=AC=√10,即⊙O的半径为√10.

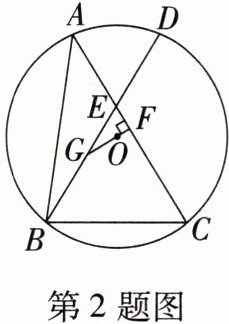
2. (2023·湖北十堰中考)如图,⊙O是△ABC的外接圆,弦BD交AC于点E,AE= DE,BC= CE,过点O作OF⊥AC于点F,延长FO交BE于点G,若DE= 3,EG= 2,则AB的长为(7)

A.4√{3}
B.7
C.8
D.4√{5}

答案： 2.B [提示:如图,连接CD,在△AEB和△DEC中,{∠A=∠D,AE=ED,∠AEB=∠DEC,
∴△AEB≌△DEC,
∴EB=EC.
∵BC=CE,
∴BE=CE=BC,
∴△EBC为等边三角形,
∴∠ACB=60°.作BM⊥AC于点M,
∵OF⊥AC,
∴AF=CF.
∵△EBC为等边三角形,
∴∠GEF=60°,
∴∠EGF=30°.
∵EG=2,
∴EF=1.
∵AE=ED=3,
∴CF=AF=4,
∴AC=8,EC=5,
∴BC=5.
∵∠BCM=60°,
∴∠MBC=30°,
∴CM=5/2,BM=√3CM=5√3/2,
∴AM=AC-CM=11/2,
∴AB=√(AM²+BM²)=√((11/2)²+(5√3/2)²)=7.

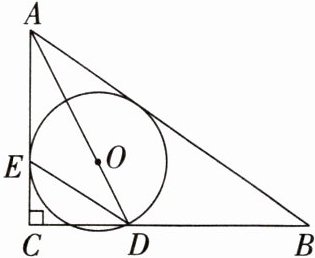
3. (2023·聊城中考)如图,在Rt△ABC中,∠ACB= 90°,∠BAC的平分线AD交BC于点D,∠ADC的平分线DE交AC于点E.以AD上的点O为圆心,OD为半径作⊙O,恰好过点E.
(1)求证：AC是⊙O的切线；
(2)若CD= 12,tan∠ABC= $\dfrac{3}{4}$,求⊙O的半径.
]

答案：
(1)证明:如图,连接OE,
∵OD=OE,
∴∠OED=∠ODE.
∵DE平分∠ADC,
∴∠CDE=∠ODE,
∴∠OED=∠CDE,
∴OE//CD.
∵∠ACB=90°,
∴∠AEO=90°,
∴OE⊥AC,又
∵OE是⊙O的半径,
∴AC是⊙O的切线.
(2)解:如图,过D作DF⊥AB,
∵AD平分∠BAC,DF⊥AB,∠ACB=90°,
∴CD=DF.
∵CD=12,tan∠ABC=3/4,
∴BF=DF/tan∠ABC=16,
∴BD=√(DF²+BF²)=20,
∴BC=CD+BD=32,
∴AC=BC·tan∠ABC=24,
∴AD=√(AC²+CD²)=12√5.
∵OE//CD,
∴△AEO∽△ACD,
∴EO/CD=AO/AD,
∴EO/12=(12√5-OD)/12√5=12√5-EO/12√5,解得EO=15-3√5,
∴⊙O的半径为15-3√5.

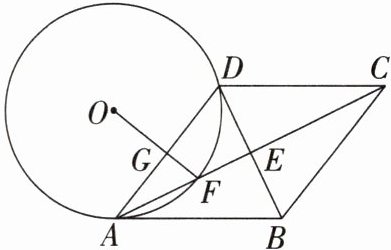
4. (2023·山东烟台中考)如图,在菱形ABCD中,对角线AC,BD相交于点E,⊙O经过A,D两点,交对角线AC于点F,连接OF交AD于点G,且AG= GD.
(1)求证：AB是⊙O的切线；
(2)已知⊙O的半径与菱形的边长之比为5:8,求tan∠ADB的值.
]

答案：
(1)证明:连接OA,则OF=OA,
∴∠OAF=∠OFA.
∵AG=GD,
∴OF⊥AD,
∴∠AGF=90°.
∵四边形ABCD是菱形,
∴AB=AD,AC⊥BD,
∴∠BAE=∠DAE,
∴∠OAB=∠OAF+∠BAE=∠OFA+∠DAE=90°,
∵OA是⊙O的半径,且AB⊥OA,
∴AB是⊙O的切线.
(2)解:
∵OA/AD=5/8,AD=2AG,
∴OA/(2AG)=5/8,
∴OA/AG=5/4.设AG=4m,则OA=5m,
∴OF=OA=5m.
∵∠AGO=90°,
∴OG=√(OA²-AG²)=√((5m)²-(4m)²)=3m,
∴FG=OF-OG=5m-3m=2m.
∵∠AED=∠AGF=90°,
∴∠ADB=∠AFG=90°-∠DAE,
∴tan∠ADB=tan∠AFG=AG/FG=4m/(2m)=2,
∴tan∠ADB的值是2.

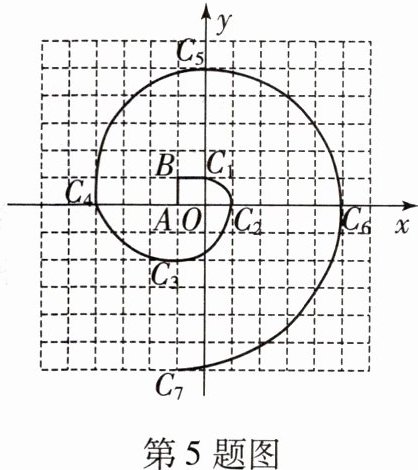
5. (2023·辽宁阜新中考)如图,四边形OABC₁是正方形,曲线C₁C₂C₃C₄C₅…叫做“正方形的渐开线”,其中$\overset{\frown}{C_{1}C_{2}}$,$\overset{\frown}{C_{2}C_{3}}$,$\overset{\frown}{C_{3}C_{4}}$,$\overset{\frown}{C_{4}C_{5}}$,…的圆心依次按O,A,B,C₁循环,当OA= 1时,点C₂₀₂₃的坐标是(-1,-2022)

A.(-1,-2022)
B.(-2023,1)
C.(-1,-2023)
D.(2022,0)

答案： 5.A [提示:由图得C₁(0,1),C₂(1,0),C₃(-1,-2),C₄(-4,1),C₅(0,5),C₆(5,0),C₇(-1,-6),…,点C的位置每4个一循环,2023=505×4+3,
∴C₂₀₂₃在第三象限,与C₃,C₇,C₁₁,…,符合规律Cₙ(-1,-n+1),
∴C₂₀₂₃的坐标为(-1,-2022).]

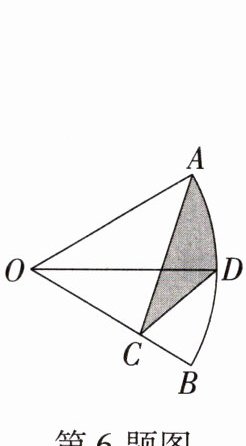
6. (2023·内蒙古通辽中考)如图,在扇形AOB中,∠AOB= 60°,OD平分∠AOB交$\overset{\frown}{AB}$于点D,点C是半径OB上一动点,若OA= 1,则阴影部分周长的最小值为(A)

A.√{2}+$\dfrac{\pi}{6}$
B.√{2}+$\dfrac{\pi}{3}$
C.2√{2}+$\dfrac{\pi}{6}$
D.2√{2}+$\dfrac{\pi}{3}$

答案： 6.A [提示:如图,作D点关于直线OB的对称点E,连接AE,与OB的交点为C点,此时阴影部分周长最小.在扇形AOB中,∠AOB=60°,OD平分∠AOB交⌒AB于点D,
∴∠AOD=∠BOD=30°.由轴对称的性质,知∠EOB=∠BOD=30°,OE=OD,
∴∠AOE=90°,
∴△AOE是等腰直角三角形.
∵OA=1,
∴AE=√2,⌒AD的长=30π×1/180=π/6,
∴阴影部分周长的最小值为√2+π/6.