第7页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. (2023·滨州惠民县自主招生)如图,在△ABC与△ADE中,∠BAC= ∠D,要使△ABC与△ADE相似,还需满足下列条件中的(
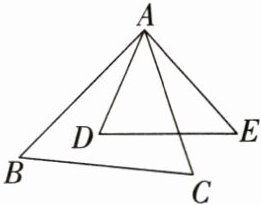
A.$\frac{AC}{AD}= \frac{AB}{AE}$
B.$\frac{AC}{AD}= \frac{BC}{DE}$
C.$\frac{AC}{AD}= \frac{AB}{DE}$
D.$\frac{AC}{AD}= \frac{BC}{AE}$
C
)
A.$\frac{AC}{AD}= \frac{AB}{AE}$
B.$\frac{AC}{AD}= \frac{BC}{DE}$
C.$\frac{AC}{AD}= \frac{AB}{DE}$
D.$\frac{AC}{AD}= \frac{BC}{AE}$
答案:
C
2. 已知在△ABC中,∠A= 78°,AB= 4,AC= 6,下列阴影部分的三角形与原△ABC不相似的是(
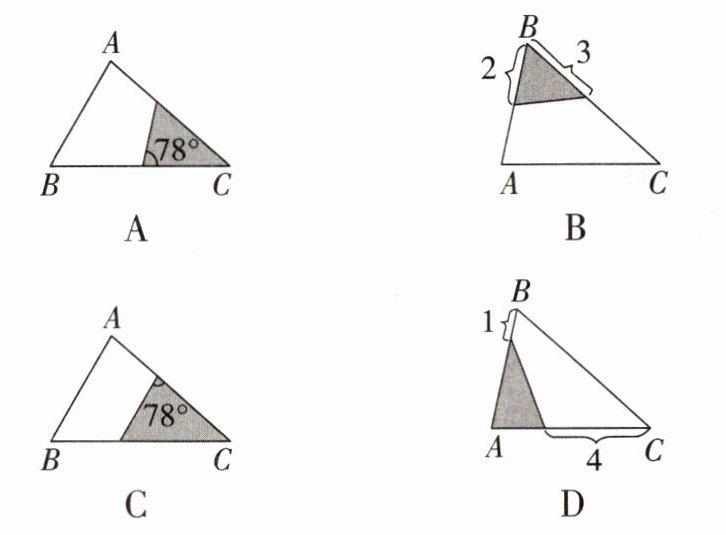
B
)
答案:
B
3. 如图,在等边三角形ABC中,D,E分别在AC,AB上,且$\frac{AD}{AC}= \frac{1}{3}$,AE= BE,则有(
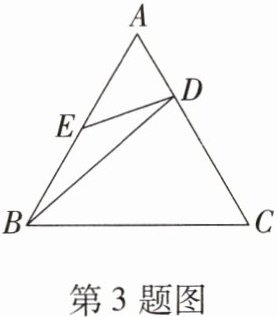
A.△AED∽△ABC
B.△ADB∽△BED
C.△BCD∽△ABC
D.△AED∽△CBD
D
)
A.△AED∽△ABC
B.△ADB∽△BED
C.△BCD∽△ABC
D.△AED∽△CBD
答案:
D
4. 如图,在正方形ABCD中,E为AB的中点,当$\frac{AF}{AD}$=
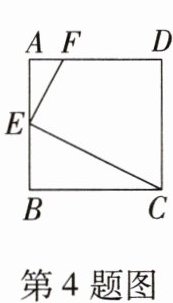
$\frac{1}{4}$
时,△AEF∽△BCE.
答案:
$\frac{1}{4}$[提示:由题意,$\angle A=\angle B=90°$,$\frac{AE}{BC}=\frac{1}{2}$,$\because\triangle AEF\backsim\triangle BCE$,$\therefore\frac{AF}{BE}=\frac{AE}{BC}=\frac{1}{2}$.$\therefore\frac{AF}{AD}=\frac{1}{4}$.]
5. 如图,已知∠BAC= ∠EAD,AB= 20.4,AC= 48,AE= 17,AD= 40. 求证:△ABC∽△AED.
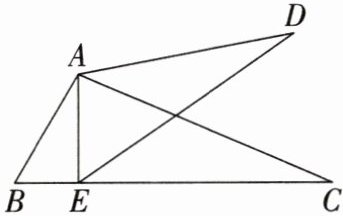

答案:
证明:$\because AB=20.4$,$AC=48$,$AE=17$,$AD=40$,$\therefore\frac{AB}{AE}=\frac{20.4}{17}=1.2$,$\frac{AC}{AD}=\frac{48}{40}=1.2$,$\therefore\frac{AB}{AE}=\frac{AC}{AD}$.$\because\angle BAC=\angle EAD$,$\therefore\triangle ABC\backsim\triangle AED$.
6. 如图,在△ABC中,$\frac{AD}{AB}= \frac{AE}{AC}= \frac{2}{3}$,若BC= 9,则DE等于(
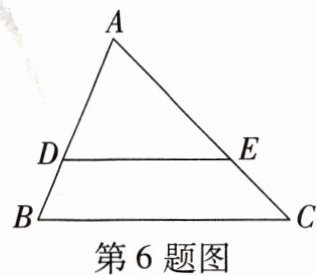
A.3
B.6
C.7
D.9
B
)
A.3
B.6
C.7
D.9
答案:
B
7. 在△ABC和△DEF中,∠A= 40°,∠D= 60°,∠E= 80°,$\frac{AB}{AC}= \frac{FD}{FE}$,那么∠B等于(
A.40°
B.60°
C.80°
D.100°
B
)A.40°
B.60°
C.80°
D.100°
答案:
B
8. 如图,在△ABC中,D,E分别是边AB,AC上的点,如果$\frac{AD}{DB}= \frac{1}{2}$,AE= 4,EC= 8,DE= 2,那么BC=
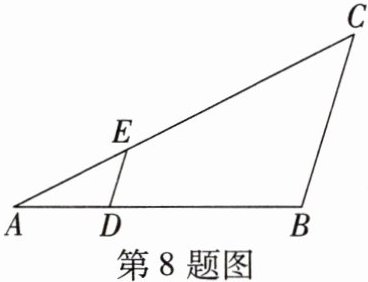
6
.
答案:
6
9. 已知AE与BD相交于点O,连接AB,DE,相关数据如图. 判断两个三角形是否相似,并求出x和y.
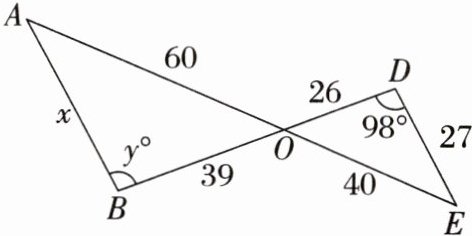

答案:
解:$\because\frac{OD}{OB}=\frac{26}{39}=\frac{2}{3}$,$\frac{OE}{OA}=\frac{40}{60}=\frac{2}{3}$,$\therefore\frac{OD}{OB}=\frac{OE}{OA}$.$\because\angle AOB=\angle EOD$,$\therefore\triangle AOB\backsim\triangle EOD$,$\therefore\frac{DE}{AB}=\frac{2}{3}$,即$\frac{27}{x}=\frac{2}{3}$,解得$x=\frac{81}{2}$,$\angle ABO=\angle EDO=98°$,即$y=98$.
查看更多完整答案,请扫码查看


