第49页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. (2023·济南历下区期末)如图,某港口$P$位于东西方向的海岸线上,甲、乙两船同时离开港口,甲船沿北偏西$50^{\circ}$方向,以每小时$12$海里的速度航行;乙船沿北偏东$40^{\circ}$方向,以每小时$16$海里的速度航行.$1小时后两船分别位于点A与B$处,此时两船相距(
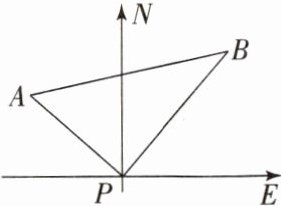
A.$12$海里
B.$16$海里
C.$20$海里
D.$24$海里
C
)
A.$12$海里
B.$16$海里
C.$20$海里
D.$24$海里
答案:
C
2. 如图,为了测量东西走向的公路桥梁$AB$的长度,数学兴趣小组在公路桥南侧选定观测点$C$,测得$A在C的北偏西37^{\circ}$方向上,点$B在C的北偏东53^{\circ}$方向上,若测得$AC = 240$m,求公路桥梁$AB$的长.(结果精确到$1$m. 参考数据:$\sin 37^{\circ}\approx 0.60$,$\cos 37^{\circ}\approx 0.80$,$\tan 37^{\circ}\approx 0.75$)
]
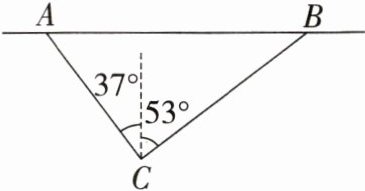
]

答案:
解:如图,作CH⊥AB于点H,则∠AHC=90°.在△ABC中,∠ACB=37°+53°=90°,
∴∠A+∠B=90°.
∵∠ACH+∠A=90°,
∴∠ABC=∠ACH=37°.
∵sin∠ABC=AC/AB,
∴AB=AC/sin37°≈240/0.60=400(m).

答:公路桥梁AB的长约为400m.
解:如图,作CH⊥AB于点H,则∠AHC=90°.在△ABC中,∠ACB=37°+53°=90°,
∴∠A+∠B=90°.
∵∠ACH+∠A=90°,
∴∠ABC=∠ACH=37°.
∵sin∠ABC=AC/AB,
∴AB=AC/sin37°≈240/0.60=400(m).

答:公路桥梁AB的长约为400m.
3. (2023·淄博淄川区期中)“淄博烧烤”火了,许多游客纷纷从外地来到淄博吃烧烤.如图,济南的小李乘坐高铁由济南来淄博吃烧烤时,在距离铁轨$200$m 的$B$处,观察他即将乘坐的由济南经过淄博开往青岛的“和谐号”动车. 他观察到,当“和谐号”动车车头在$A$处时,恰好位于$B处的北偏东60^{\circ}$方向上,$10$s 后,动车车头到达$C$处,恰好位于$B$处的西北方向上,则这时段动车的平均速度是(
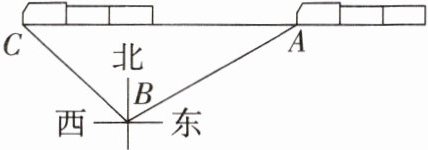
A.$20(\sqrt{3} + 1)$m/s
B.$20(\sqrt{3} - 1)$m/s
C.$200$m/s
D.$300$m/s
A
)
A.$20(\sqrt{3} + 1)$m/s
B.$20(\sqrt{3} - 1)$m/s
C.$200$m/s
D.$300$m/s
答案:
A[提示:作BD⊥AC于点D.
∵在Rt△ABD中,∠ABD=60°,
∴AB=2BD=400,AD=√(AB² - BD²)=200√3.同理,CD = BD = 200.则AC = 200 + 200√3.
∴这时段动车的平均速度是(200 + 200√3)/10 = 20(√3 + 1)(m/s).]
∵在Rt△ABD中,∠ABD=60°,
∴AB=2BD=400,AD=√(AB² - BD²)=200√3.同理,CD = BD = 200.则AC = 200 + 200√3.
∴这时段动车的平均速度是(200 + 200√3)/10 = 20(√3 + 1)(m/s).]
4. 如图,一艘货轮在上午$8:00时位于A$处,沿$A到B$的方向航行,当日上午$10:00时该货轮位于B$处,求该货轮在这段时间内航行的平均速度.
]
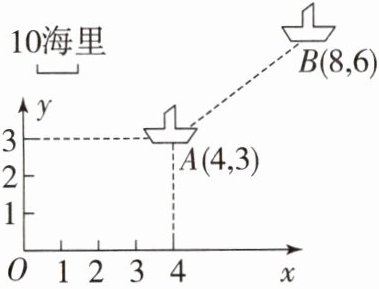
]

答案:
解:如图,过点A作x轴的平行线、过点B作x轴的垂线,两线相交于点C,则AC = 80 - 40 = 40,BC = 60 - 30 = 30.由勾股定理得AB = √(AC² + BC²)=50,
∴50÷2 = 25(海里/时).

答:该货轮在这段时间内航行的平均速度为每小时25海里.
解:如图,过点A作x轴的平行线、过点B作x轴的垂线,两线相交于点C,则AC = 80 - 40 = 40,BC = 60 - 30 = 30.由勾股定理得AB = √(AC² + BC²)=50,
∴50÷2 = 25(海里/时).

答:该货轮在这段时间内航行的平均速度为每小时25海里.
5. 如图,一艘轮船以$40$海里/时的速度在海面上航行,当它行驶到$A$处时,发现它的北偏东$30^{\circ}方向有一灯塔B$. 轮船继续向北航行$2小时后到达C$处,发现灯塔$B在它的北偏东60^{\circ}$方向. 若轮船继续向北航行,则到达离灯塔$B$最近位置,需要的时间是(
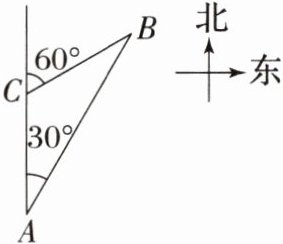
A.$1$小时
B.$\sqrt{3}$小时
C.$2$小时
D.$2\sqrt{3}$小时
A
)
A.$1$小时
B.$\sqrt{3}$小时
C.$2$小时
D.$2\sqrt{3}$小时
答案:
A
6. 如图,$C$处是一海上钻井平台,位于东营港口$A的北偏东60^{\circ}$方向上,与港口$A相距60\sqrt{2}$海里,一艘摩托艇从$A$出发,自西向东航行至$B$时,改变航向以每小时$50海里的速度沿BC$方向行进,此时$C位于B的北偏西45^{\circ}$方向上,则从$B处到达C$处需要多少小时?
]
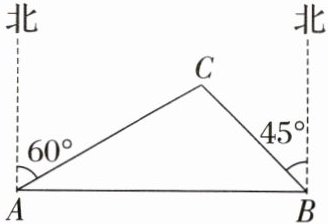
]

答案:
解:过C作CD⊥AB于D,在点A的正北方向上取点M,在点B的正北方向上取点N,由题意得∠MAB = ∠NBA = 90°,∠MAC = 60°,∠NBC = 45°,AC = 60√2海里.在Rt△ACD中,
∵∠CAD = ∠MAB - ∠MAC = 90° - 60° = 30°,
∴CD = 1/2AC = 30√2(海里).在Rt△BCD中,
∵∠CDB = 90°,∠CBD = ∠NBD - ∠NBC = 90° - 45° = 45°,
∴BC = √2CD = 60(海里),60÷50 = 1.2(小时),
∴从B处到达C处需要1.2小时到达B处.
∵∠CAD = ∠MAB - ∠MAC = 90° - 60° = 30°,
∴CD = 1/2AC = 30√2(海里).在Rt△BCD中,
∵∠CDB = 90°,∠CBD = ∠NBD - ∠NBC = 90° - 45° = 45°,
∴BC = √2CD = 60(海里),60÷50 = 1.2(小时),
∴从B处到达C处需要1.2小时到达B处.
查看更多完整答案,请扫码查看


