《2025年全科王同步课时练习九年级数学上册青岛版》

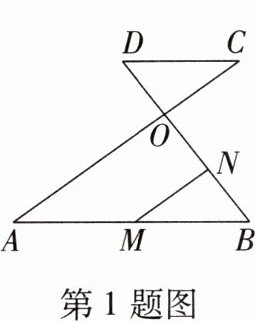
1. (2023·黑龙江哈尔滨中考)如图,AC,BD相交于点O,AB// DC,M是AB的中点,MN// AC,交BD于点N,若DO:OB= 1:2,AC= 12,则MN的长为 (B)

A.2
B.4
C.6
D.8

答案： B

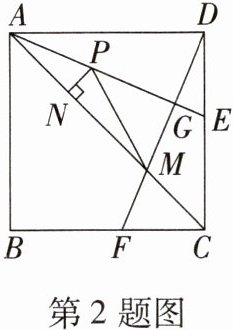
2. (2023·东营中考)如图,正方形ABCD的边长为4,点E,F分别在边DC,BC上,且BF= CE,AE平分∠CAD,连接DF,分别交AE,AC于点G,M,P是线段AG上的一个动点,过点P作PN⊥AC,垂足为N,连接PM.有下列四个结论:
①AE垂直平分DM;
②PM+PN的最小值为3√2;
$③CF^2= GE·AE;$
$④S_{△ADM}= 6√2.$
其中正确的是 (①③)

A.①②
B.②③④
C.①③④
D.①③

答案： D[提示:①在正方形ABCD中,易得CF=DE,由△ADE≌△DCF,易得△AGM≌△AGD,
∴GM=GD.又
∵∠AGM=∠AGD=90°,
∴AE垂直平分DM,故①正确.②如图，连接BD与AC交于点O,交AG于点H,连接HM,则AC⊥BD,即DO⊥AM,由AE垂直平分DM,得HM=HD.当点P与点H重合时，PM+PN的值最小,此时PM+PN=HM+HO=HD+HO=DO,即PM+PN的最小值是DO的长.
∵正方形ABCD的边长为4,
∴BD=4√2,
∴DO=$\frac{1}{2}$BD=2√2,即PM+PN的最小值为2√2,故②错误.③
∵AE垂直平分DM,
∴∠DGE=90°.
∵∠ADE=90°,
∴∠DGE=∠ADE.又
∵∠DEG=∠AED,
∴△DGE∽△ADE,
∴$\frac{DE}{AE}$=$\frac{GE}{DE}$,即DE²=GE·AE,由①知CF=DE,
∴CF²=GE·AE,故③正确.④
∵AE垂直平分DM,
∴AM=AD=4,又DO=2√2,
∴S△ADM=$\frac{1}{2}$AM·DO=$\frac{1}{2}$×4×2√2=4√2,故④错误.综上,正确的是①③.]

3. (2023·黑龙江大庆中考)在综合与实践课上,老师组织同学们以“矩形的折叠”为主题开展数学活动.有一张矩形纸片ABCD如图,点N在边AD上,现将矩形折叠,折痕为BN,点A对应的点记为M,若点M恰好落在边DC上,则图中与△NDM一定相似的三角形是△MCB.

答案： △MCB[提示:
∵四边形ABCD是矩形，
∴∠A=∠D=∠C=90°,
∴∠DNM+∠DMN=90°.由折叠的性质知∠BMN=∠A=90°,
∴∠DMN+∠CMB=90°,
∴∠DNM=∠CMB,
∴△NDM∽△MCB.]

4. (2023·广东中考)边长分别为10,6,4的三个正方形拼接在一起,它们的底边在同一直线上(如图),则图中阴影部分的面积为15.

答案： 15[提示:如图，
∵BF//DE,
∴△ABF∽△ADE,
∴$\frac{AB}{AD}$=$\frac{BF}{DE}$.
∵AB=4,AD=4+6+10=20,DE=10,
∴$\frac{4}{20}$=$\frac{BF}{10}$,
∴BF=2,
∴GF=6−2=4.
∵CK//DE,
∴△ACK∽△ADE,
∴$\frac{AC}{AD}$=$\frac{CK}{DE}$.
∵AC=4+6=10,AD=20,DE=10,
∴$\frac{10}{20}$=$\frac{CK}{10}$,
∴CK=5,
∴HK=6−5=1,
∴阴影部分(梯形)的面积=$\frac{1}{2}$(HK+GF)·GH=$\frac{1}{2}$×(1+4)×6=15.]

5. (2023·辽宁本溪中考)如图,在平面直角坐标系中,四边形OABC的顶点坐标分别是O(0,0),A(1,0),B(2,3),C(-1,2),若四边形OA'B'C'与四边形OABC关于原点O位似,且四边形OA'B'C'的面积是四边形OABC面积的4倍,则第一象限内点B'的坐标为(4,6).

答案： (4,6)[提示:
∵四边形OA'B'C'与四边形OABC关于原点O位似，且四边形OA'B'C'的面积是四边形OABC面积的4倍，
∴四边形OA'B'C'与四边形OABC的相似比是2:1.
∵点B(2,3),
∴第一象限内点B'的坐标为(4,6).]

6. (2023·黑龙江绥化中考)如图,在平面直角坐标系中,△ABC与△AB'C'的相似比为1:2,点A是位似中心,已知点A(2,0),点C(a,b),∠C= 90°,则点C'的坐标为______.(结果用含a,b的式子表示)

答案： (6−2a,−2b)[提示:如图，过C作CM⊥AB于M,过C'作C'N⊥AB'于N,则∠ANC'=∠AMC=90°.
∵△ABC与△AB'C'的相似比为1:2,
∴$\frac{AC}{AC'}$=$\frac{1}{2}$.
∵∠CAM=∠NAC',
∴△ACM∽△AC'N,
∴$\frac{AM}{AN}$=$\frac{CM}{C'N}$=$\frac{AC}{AC'}$.
∵点A(2,0),点C(a,b),
∴OA=2,OM=a,CM=b,
∴AM=a−2,
∴$\frac{a−2}{AN}$=$\frac{b}{C'N}$=$\frac{1}{2}$,
∴AN=2a−4,C'N=2b,
∴ON=AN−OA=2a−6,
∴点C'的坐标为(6−2a,−2b).]

7. (探究题)[2023·烟台中考]如图,在平面直角坐标系中,网格内每个小正方形的边长均为1个单位长度,以点P为位似中心作正方形PA₁A₂A₃,正方形PA₄A₅A₆,…,按此规律作下去,所作正方形的顶点均在格点上,其中正方形PA₁A₂A₃的顶点坐标分别为P(-3,0),A₁(-2,1),A₂(-1,0),A₃(-2,-1),则顶点$A_{100}$的坐标为 (31,34)
A.(31,34)
B.(31,-34)
C.(32,35)
D.(32,0)

答案： A[提示:由题意知,A₁₊₃ₙ(n为非负整数)在射线PA₁上，
∵100=1+3×33,
∴n=33,
∵A₁(−2,1),A₄(−1,2),A₇(0,3),...,
∴A₁₊₃ₙ(n−2,n+1),
∴顶点A₁₀₀的坐标为(33−2,33+1),即(31,34).]