《2025年全科王同步课时练习九年级数学上册青岛版》

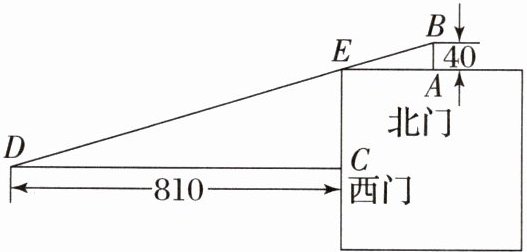
7. 《九章算术》中记载：“今有邑方不知大小,各开中门,出北门四十步有木,出西门八百一十步见木,问：邑方几何?”译文：如图,一座正方形城池北、西边正中A,C处各开一道门,从点A往正北方向走40步刚好有一棵树位于点B处,若从点C往正西方向走810步到达点D处时正好看到此树,则正方形城池的边长为(360步)

A.360步
B.270步
C.180步
D.90步
]

答案： A[提示:设正方形城池的边长为x步,则AE=CE=$\frac{1}{2}$x.
∵AE//CD,
∴∠BEA=∠EDC,又∠BAE=∠ECD,
∴△BEA∽△EDC,
∴$\frac{AB}{EC}$=$\frac{AE}{CD}$,即$\frac{40}{\frac{1}{2}x}$=$\frac{\frac{1}{2}x}{810}$,
∴x=360,即正方形城池的边长为360步.]

8. 如图是用杠杆撬石头的示意图,C是支点,当用力压杠杆的A端时,杠杆绕C点转动,另一端B向上翘起,石头就被撬动.现有一块石头,要使其滚动,杠杆的B端必须至少向上翘起10cm,已知杠杆的动力臂AC与阻力臂BC之比为6:1,要使这块石头滚动,至少要将杠杆的A端向下压60cm.
]

答案： 60cm[提示:如图,AM,BN都与水平线垂直，即AM//BN.
∵AM//BN,
∴△ACM∽△BCN,
∴$\frac{AC}{BC}$=$\frac{AM}{BN}$.
∵AC与BC之比为6:1,
∴$\frac{AC}{BC}$=$\frac{AM}{BN}$=6,即AM=6BN,
∴当BN≥10cm时,AM≥60cm,故要使这块石头滚动，至少要将杠杆的A端向下压60cm.]

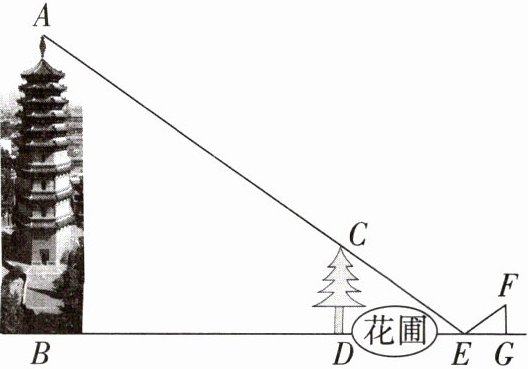
9. 某数学兴趣小组要完成一个项目学习,测量凌霄塔的高度AB.如图,塔前有一棵高4m的小树CD,发现水平地面上点E、树顶C和塔顶A恰好在一条直线上,测得BD= 57m,D,E之间有一个花圃距离无法测量；然后在E处放置一平面镜,沿BE后退,退到G处恰好在平面镜中看到树顶C的像,EG= 2.4m,测量者眼睛到地面的距离FG为1.6m.已知AB⊥BG,CD⊥BG,FG⊥BG,点B,D,E,G在同一水平线上.求凌霄塔的高度AB.(平面镜的大小、厚度忽略不计)

答案： 解:
∵CD⊥BG,FG⊥BG,
∴∠CDE=∠FGE=90°.
∵∠FEG =∠CED,
∴△CDE∽△FGE,
∴$\frac{CD}{FG}$=$\frac{DE}{EG}$.
∵CD=4,FG=1.6,EG=2.4,
∴$\frac{4}{DE}$=$\frac{1.6}{2.4}$,解得DE=6.
∵BD=57,
∴BE=BD + DE=57 + 6=63.
∵AB⊥BG,CD⊥BG,
∴∠ABE=∠CDE=90°.
∵∠AEB=∠CED,
∴△ABE∽△CDE,
∴$\frac{AB}{BE}$=$\frac{CD}{DE}$,即$\frac{AB}{63}$=$\frac{4}{6}$,解得AB=42,
∴凌霄塔的高度AB为42m.

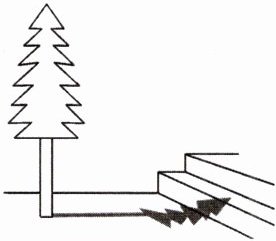
10. 兴趣小组的同学要测量教学楼前一棵树的高度.在阳光下,一名同学测得一根直立在地面上的长为1米的竹竿在地面上的影长为0.4米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此台阶水平面上的影子长为0.2米,一级台阶高为0.3米,如图,若此时落在地面上的影长为4.4米,则此树高为多少米?
]

答案： 解法1:根据题意可构造相似三角形模型如图
(1),其中AB为树高，EF为树影在第一级台阶上的影长，BD为树影在地上部分的长，ED的长为台阶高，并且由光沿直线传播的性质可知BC即为树影在地上的全长.延长FE交AB于G，则△ABC∽△AGF.
∴AG:GF=AB:BC=物高:影长=1:0.4,
∴GF=0.4AG.又
∵GF=GE+EF,BD=GE,BD=4.4米,EF=0.2米,
∴GF=4.6米,AG=11.5米,
∴AB=AG+GB=11.8米,即树高为11.8米.解法2:如图
(2),由题意可得DG=0.2米,DE=0.3米,AE=4.4米.
∵$\frac{DE}{EH}$=$\frac{1}{0.4}$,
∴EH=0.3×0.4=0.12(米).
∵DG=HF=0.2米,
∴AF=AE+EH+HF=4.4+0.12+0.2=4.72(米).
∵$\frac{AB}{AF}$=$\frac{1}{0.4}$,
∴AB=$\frac{4.72}{0.4}$=11.8(米).即树高为11.8米.