《2025年全科王同步课时练习九年级数学上册青岛版》

11. 如图,在$\odot O$中,$BC$是直径,$AB = DC$,则下列结论不一定成立的是 (A)

A.$OA = OB = AB$
B.$\angle AOB = \angle COD$
C.$\overset{\frown}{AB} = \overset{\frown}{DC}$
D.$O到AB$,$CD$的距离相等

答案： A

12. 如图,将大小不同的两块量角器的零度线对齐,且小量角器的中心$O_{2}$恰好在大量角器的圆周上,设图中两圆周的交点为P,且点P在小量角器上对应的刻度为63°,那么点P在大量角器上对应的刻度为(只考虑小于$90^{\circ}$的角) (A)

A.$54^{\circ}$
B.$55^{\circ}$
C.$56^{\circ}$
D.$57^{\circ}$

答案： A[提示:连接 OP,O₂P,
∵P 在小量角器上对应的刻度为 63°,
∴∠OO₂P = 63°.
∵OP = O₁O₂,
∴∠OPO₂ = ∠OO₂P = 63°,
∴∠PO₁O₂ = 180° - 63° - 63° = 54°,即点 P 在大量角器上对应的刻度为 54°.]

13. 如图,点$A在半圆O$上,$BC$是直径,$\overset{\frown}{AB} = \overset{\frown}{AC}$. 若$AB = 2$,则$BC$的长为2√2.

答案： 2√2[提示:连接 OA,
∵AB = AC,BC 是直径,
∴OA⊥BC.
∵OA = OB,AB = 2,
∴OA = OB = $\frac{\sqrt{2}}{2}$AB = $\frac{\sqrt{2}}{2}$×2 = √2,
∴BC = 2OB = 2√2.]

14. 如图,在$\odot O$中,$\overset{\frown}{AC} = \overset{\frown}{BC}$,$OD = \frac{1}{2}AO$,$OE = \frac{1}{2}OB$,求证：$CD = CE$.

答案： 证明:
∵AC = BC,
∴∠AOC = ∠BOC.
∵OD = $\frac{1}{2}$AO,OE = $\frac{1}{2}$OB,OA = OB,
∴OD = OE.在△COD 与△COE 中,
∵OD = OE,∠DOC = ∠EOC,OC = OC,
∴△COD ≌ △COE,
∴CD = CE.

15. (2023·潍坊寒亭区期中)如图,在直径为$20的\odot O$中,$AB与CD$是互相垂直的两条弦,垂足为点$F$. 已知$AB = CD = 16$,求$OF$的长.

答案：
解:过 O 点作 OM⊥AB 于 M 点,ON⊥CD 于 N 点,连接 OA,如图,
∴∠OMF = ∠ONF = 90°,AM = BM = 8.
∵AB⊥CD,
∴∠MFN = 90°,

∴四边形 OMFN 是矩形.
∵AB = CD,
∴OM = ON,
∴四边形 OMFN 是正方形,
∴OM = MF.
∵直径为 20,
∴OA = 10.在 Rt△AOM 中,OM = $\sqrt{OA^{2}-AM^{2}}$ = $\sqrt{10^{2}-8^{2}}$ = 6,
∴MF = 6.在 Rt△OMF 中,OF = $\sqrt{OM^{2}+MF^{2}}$ = $\sqrt{6^{2}+6^{2}}$ = 6√2,即 OF 的长为 6√2.

16. 一次综合实践的主题为“只用一张矩形纸条和刻度尺,如何测量如图①的一次性纸杯杯口的直径?”小明同学所在的学习小组想到了如下方法：如图②,将纸条拉直紧贴杯口上,纸条的上下边分别与杯口相交于$A$,$B$,$C$,$D$四点,利用刻度尺量得该纸条宽为$3.5\ cm$,$AB = 3\ cm$,$CD = 4\ cm$. 请你帮忙计算纸杯杯口的直径.

答案：
解:如图,作 MN⊥AB,MN 过圆心 O 且分别与 CD,AB 交于 M,N,连接 OD,OB,

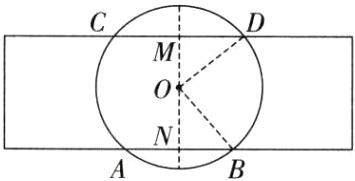
∴MN = 3.5cm.
∵CD//AB,
∴MN⊥CD,
∴DM = $\frac{1}{2}$CD = $\frac{1}{2}$×4 = 2(cm),BN = $\frac{1}{2}$AB = $\frac{1}{2}$×3 = 1.5(cm).设 OM = x cm,
∴ON = MN - OM = (3.5 - x)cm.
∵OM² + MD² = OD²,ON² + BN² = OB²,
∴OM² + MD² = ON² + BN²,
∴x² + 2² = (3.5 - x)² + 1.5²,
∴x = 1.5,
∴OM = 1.5(cm),
∴OD = $\sqrt{OM² + MD²}$ = $\sqrt{1.5² + 2²}$ = 2.5(cm),
∴纸杯杯口的直径为 2.5×2 = 5(cm).