《2025年全科王同步课时练习九年级数学上册青岛版》

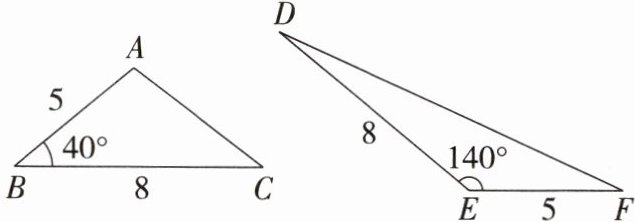
11. 如图,若△ABC 和△DEF 的面积分别为$ S_1,S_2,$则$ S_1 : S_2 $等于( )


A.5 : 8
B.8 : 5
C.1 : 1
D.2 : 7

答案：
C[提示:如图①,过 A 作 AM⊥BC 于 M,如图②,过 D 作 DN⊥FE 交 FE 延长线于 N,
∵ sinB=sin40°=AM/AB,
∴ AM=AB·sin40°=5sin40°,
∴ S△ABC=1/2BC·AM=1/2×8×5sin40°=20sin40°.
∵ ∠DEF=140°,
∴ ∠DEN=180° - 140°=40°.
∵ sin∠DEN=sin40°=DN/DE,
∴ DN=DE·sin40°=8sin40°,
∴ S△DEF=1/2EF·DN=1/2×5×8sin40°=20sin40°,
∴ S△ABC=S△DEF,
∴ S₁:S₂=1:1.]

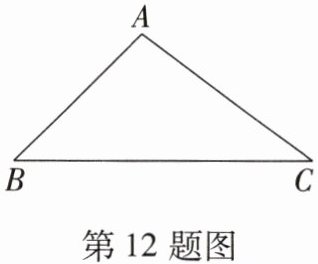
12. (2023·聊城东昌府区校级月考)如图,在△ABC 中,AC = 5,cos B = $\frac{\sqrt{2}}{2}$,sin C = $\frac{3}{5}$,则△ABC 的面积是($\frac{21}{2}$)

A.14
B.12
C.$\frac{21}{2}$
D.21

答案： C[提示:过 A 作 AD⊥BC 于点 D,
∵ △ABC 中,AC=5,cosB=√2/2,sinC=3/5,
∴ AD/AC=3/5,得 AD=3,∠B=45°,
∴ tanB=AD/BD=tan45°,得 BD=3,CD=√(AC² - AD²)=√(5² - 3²)=4,
∴ S△ABC=(BD + CD)·AD/2=(3 + 4)×3/2=21/2.]

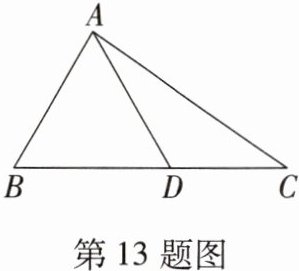
13. 如图,在△ABC 中,AB = 4,BC = 7,∠B = 60°,点 D 在边 BC 上,CD = 3,连接 AD. 如果将△ACD 沿直线 AD 翻折后,点 C 的对应点为 E,那么点 E 到直线 BD 的距离为______.

答案：
3√3/2[提示:如图,过点 E 作 EH⊥BC 于 H.
∵ BC=7,CD=3,
∴ BD=BC - CD=4.
∵ AB=4=BD,∠B=60°,
∴ △ABD 是等边三角形,
∴ ∠ADB=60°,
∴ ∠ADC=∠ADE=120°,
∴ ∠EDH=60°.
∵ DE=DC=3,
∴ EH=DE·sin60°=3√3/2,
∴ E 到直线 BD 的距离为 3√3/2.]

14. 在△ABC 中,tan A = $\frac{\sqrt{3}}{3}$,tan B = 1,CD ⊥ AB 于点 D,且 BD = 4,请画出示意图并且求边 AB 的长.

答案：
:如图,
∵ tanA=√3/3,
∴ ∠A=30°,
∵ tanB=1,
∴ ∠B=45°.
∵ CD⊥AB,
∴ ∠CDB=90°,
∴ ∠DCB=∠B=45°,
∴ CD=BD=4.在 Rt△ADC 中,AD=CD/tan30°=4√3,
∴ AB=BD+AD=4+4√3.即边 AB 的长为 4+4√3.

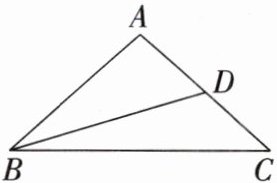
15. 如图,在△ABC 中,AB = AC = 5,BC = 8,点 D 是边 AC 的中点,连接 BD,求∠DBC 的正弦值.

答案：
解:过 A 作 AM⊥BC 于 M,过 D 作 DN⊥BC 于 N,如图,
∵ AB=AC=5,BC=8,AM⊥BC,
∴ BM=CM=1/2BC=4,
∴ AM=√(AB² - BM²)=√(5² - 4²)=3.
∵ 点 D 是边 AC 的中点,AM//DN,
∴ CD=1/2AC=5/2,DN 是△ACM 的中位线,
∴ DN=1/2AM=3/2,CN=1/2CM=2,
∴ BN=BC - CN=8 - 2=6.在 Rt△DBN 中,BD=√(BN² + DN²)=√(6²+(3/2)²)=3√17/2,
∴ sin∠DBN=DN/BD=3/2÷3√17/2=√17/17.

16. 如图①,由直角三角形边角关系,可将三角形面积公式变形得到 $ S_{△ABC} = \frac{1}{2}bc\sin A $,① 即三角形的面积等于两边之长与夹角正弦值之积的一半.
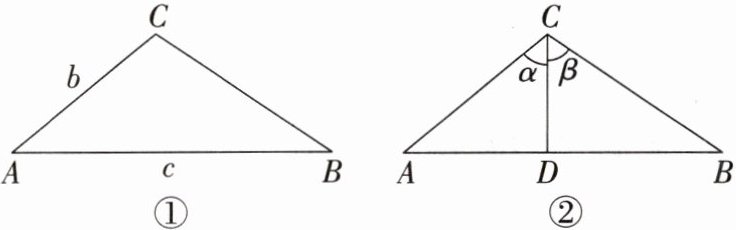
如图②,在△ABC 中,CD ⊥ AB 于 D,∠ACD = α,∠DCB = β. ∵ $ S_{△ABC} = S_{△ACD} + S_{△BCD} $,由①得到 $ \frac{1}{2}AC·BC·\sin(\alpha + \beta) = \frac{1}{2}AC·CD·\sin \alpha + \frac{1}{2}BC·CD·\sin \beta $,即 $ AC·BC·\sin(\alpha + \beta) = AC·CD·\sin \alpha + BC·CD·\sin \beta $. ② 你能利用直角三角形的相关知识及等式基本性质,消去②中的 AC,BC,CD 吗？若不能,说明理由；若能,写出解决过程,并利用结论求 sin 75°的值.

答案： 解:能消去②中的 AC,BC,CD.将 AC·BC·sin(α+β)=AC·CD·sinα+BC·CD·sinβ,两边同除以 AC·BC 得 sin(α+β)=CD/BC·sinα+CD/AC·sinβ,③ 又 cosβ=CD/BC,cosα=CD/AC,代入③可得 sin(α+β)=sinα·cosβ+cosα·sinβ.由 sin(α+β)=sinα·cosβ+cosα·sinβ 得 sin75°=sin(30°+45°)=sin30°·cos45°+cos30°·sin45°=1/2×√2/2+√3/2×√2/2=(√2+√6)/4.