《2025年全科王同步课时练习九年级数学上册青岛版》

1. 如图,在菱形 $ABCD$ 中,$EF\perp AC$ 于点 $H$,分别交 $AD$ 于点 $E$,交 $AB$ 于点 $G$,交 $CB$ 的延长线于点 $F$,且 $AE:FB = 1:3$,则 $GB:CD$ 的值为(D)

A.$\frac{1}{5}$
B.$\frac{4}{5}$
C.$\frac{2}{3}$
D.$\frac{3}{4}$

答案： D

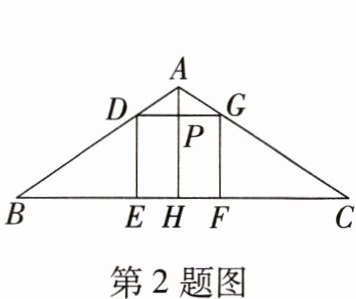
2. 如图,正方形 $DGFE$ 的边 $EF$ 在 $\triangle ABC$ 的边 $BC$ 上,顶点 $D$,$G$ 分别在边 $AB$,$AC$ 上,$AH\perp BC$ 于 $H$,交 $DG$ 于 $P$,且 $BC = 48$,$AH = 16$,那么 $S_{正方形DGFE}= $144。

答案： 144 [提示:设正方形 DGFE 的边长为 x. 由正方形 DEFG 得 DG//EF,即 DG//BC.
∵ AH⊥BC,
∴ AP⊥DG.
∵ DG//BC,
∴△ADG∽△ABC,
∴ DG/BC = AP/AH,即 DG/BC = (AH - PH)/AH.
∵ PH⊥BC,DE⊥BC,
∴ PH = ED.由 BC = 48,AH = 16,DE = DG = PH = x,得 x/48 = (16 - x)/16,解得 x = 12.
∴ 正方形 DEFG 的边长是 12,
∴ S正方形DGFE = DE² = 12² = 144.]

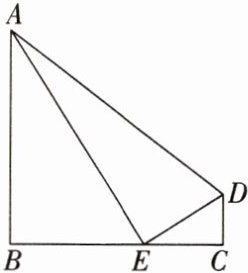
3. (2023·淄博期末)如图,$AB\perp BC$,$DC\perp BC$,$E$ 是 $BC$ 上一点,使得 $AE\perp DE$。
(1)求证：$\triangle ABE\backsim\triangle ECD$；
(2)若 $AB = 4$,$AE = BC = 5$,求 $CD$ 的长；
(3)当 $\triangle AED\backsim\triangle ECD$ 时,请写出线段 $AD$,$AB$,$CD$ 之间的数量关系,并说明理由。
]

答案：
(1)证明:
∵ AB⊥BC,DC⊥BC,
∴ ∠B = ∠C = 90°,∠BAE + ∠AEB = 90°.
∵ AE⊥DE,
∴ ∠AED = 90°,
∴ ∠AEB + ∠DEC = 90°,
∴ ∠DEC = ∠BAE,
∴△ABE∽△ECD.
(2)解:在 Rt△ABE 中,
∵ AB = 4,AE = 5,
∴ BE = 3.
∵ BC = 5,
∴ EC = 5 - 3 = 2.由
(1)得△ABE∽△ECD,
∴ AB/BE = EC/CD,
∴ 4/3 = 2/CD,
∴ CD = 3/2.
(3)解:线段 AD,AB,CD 之间的数量关系为 AD = AB + CD.理由如下:过 E 作 EF⊥AD 于 F,
∵△AED∽△ECD,
∴ ∠ADE = ∠EDC.
∵ DC⊥BC,
∴ EF = EC.
∵ DE = DE,
∴ Rt△DFE≌Rt△DCE,
∴ DF = DC.同理可得 Rt△ABE≌Rt△AFE,
∴ AB = AF,
∴ AD = AF + DF = AB + CD. [解题方法] 本题
(3)中注意作辅助线将 AD 分成两条线段.

4. (2023·潍坊临朐县期末)[多选题]如图,在 $\triangle ABC$ 中,$AB = 4\ cm$,$AC = 3\ cm$,$BC = 6\ cm$,$D$ 是 $AC$ 上一点,$AD = 2\ cm$,点 $P$ 从 $C$ 出发沿 $C\rightarrow B\rightarrow A$ 方向,以 $1\ cm/s$ 的速度匀速运动至点 $A$ 处,线段 $DP$ 将 $\triangle ABC$ 分成两部分,其中一部分与 $\triangle ABC$ 相似,则运动时间可能是(AC)

A.$\frac{1}{2}\ s$
B.$3\ s$
C.$\frac{22}{3}\ s$
D.$8\ s$

答案： AC [提示:设点 P 的运动时间为 t s,如图①,当△CPD∽△CAB 时,有 CP/CA = CD/CB,
∴ t/3 = 1/6,
∴ t = 1/2.当△CDP'∽△CAB 时,有 CP'/CB = CD/CA,
∴ t/6 = 1/3,
∴ t = 2.如图②,当△ADP∽△ACB 时,有 AP/AB = AD/AC,
∴ (10 - t)/4 = 2/3,
∴ t = 22/3.当△ADP'∽△ABC 时,有 AP'/AC = AD/AB,
∴ (10 - t)/3 = 2/4,
∴ t = 17/2.]

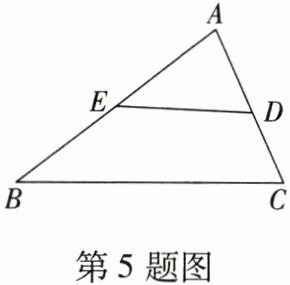
5. 如图,在 $\triangle ABC$ 中,$AB = 6$,$CA = 4$,点 $D$ 为 $AC$ 的中点,点 $E$ 在 $AB$ 上,当 $AE = $3 或 4/3时,$\triangle ABC$ 与以点 $A$,$D$,$E$ 为顶点的三角形相似。

答案： 3 或 4/3 [提示:当 AE/AD = AB/AC 时,
∵ ∠A = ∠A,
∴△AED∽△ABC,
∴ AE = (AB·AD)/AC = (6×2)/4 = 3.当 AD/AE = AB/AC 时,
∵ ∠A = ∠A,
∴△ADE∽△ABC,
∴ AE = (AC·AD)/AB = (4×2)/6 = 4/3.综上,AE = 3 或 4/3.]

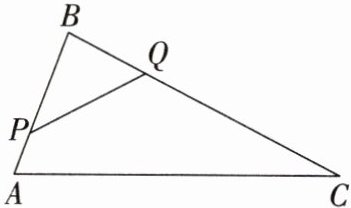
6. 如图,在 $\triangle ABC$ 中,$AB = 4\ cm$,$BC = 8\ cm$,点 $P$ 从点 $A$ 开始沿 $AB$ 边向点 $B$ 以 $1\ cm/s$ 的速度匀速移动,点 $Q$ 从点 $B$ 开始沿 $BC$ 边向点 $C$ 以 $2\ cm/s$ 的速度匀速移动,$P$,$Q$ 分别从 $A$,$B$ 同时出发,经过几秒后,点 $P$,$B$,$Q$ 构成的三角形与 $\triangle ABC$ 相似？
]

答案： 解:设经过 t s 后,点 P,B,Q 构成的三角形与△ABC 相似,则 AP = t,BQ = 2t.①当 BP 与 BA 是对应边时,△BPQ∽△BAC,
∴ PB/AB = BQ/BC,
∴ (4 - t)/4 = 2t/8,解得 t = 2.②当 BP 与 BC 是对应边时,△BPQ∽△BCA,
∴ PB/BC = BQ/AB,
∴ (4 - t)/8 = 2t/4,解得 t = 0.8.
∴ 经过 0.8 s 或 2 s 后,点 P,B,Q 构成的三角形与△ABC 相似.