第52页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
6. 桔槔俗称“吊杆”“称杆”(如图①),是我国古代农用工具,始见于《墨子·备城门》,是一种利用杠杆原理的取水机械。桔槔示意图如图②, $ OM $ 是垂直于水平地面的支撑杆, $ OM = 3\mathrm{m} $, $ AB $ 是杠杆, $ AB = 6\mathrm{m} $, $ OA:OB = 2:1 $。当点 $ A $ 位于最高点时, $ \angle AOM = 120^{\circ} $,此时,点 $ A $ 到地面的距离为(
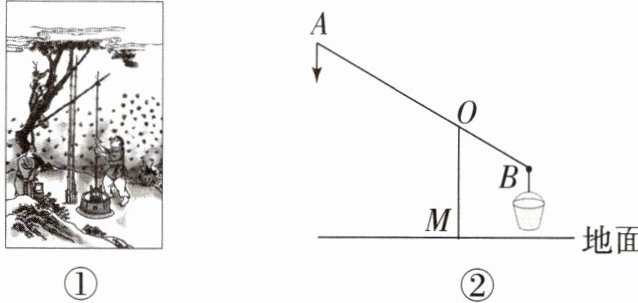
A.$ (2\sqrt{3} + 3)\mathrm{m} $
B.$ 5\mathrm{m} $
C.$ 6\mathrm{m} $
D.$ 7\mathrm{m} $
5m
)
A.$ (2\sqrt{3} + 3)\mathrm{m} $
B.$ 5\mathrm{m} $
C.$ 6\mathrm{m} $
D.$ 7\mathrm{m} $
答案:
B[提示:如图,过O作EF⊥OM,过A作AG⊥EF于G,
∵AB =6m,OA:OB=2:1,
∴OA=4m.
∵∠AOM=120°,∠EOM=90°,
∴∠AOE=30°.在Rt△AOG中,AG=AO·sin30°=2(m),点A位于最高点时到地面的距离为2+3=5(m).]
∵AB =6m,OA:OB=2:1,
∴OA=4m.
∵∠AOM=120°,∠EOM=90°,
∴∠AOE=30°.在Rt△AOG中,AG=AO·sin30°=2(m),点A位于最高点时到地面的距离为2+3=5(m).]
7. 如图,准备在宽 $ 24\mathrm{m} $ 的迎宾大道 $ AB $ 路边安装路灯,设计要求:路灯的灯臂 $ CD $ 长 $ 4\mathrm{m} $,且与灯柱 $ BC $ 成 $ 120^{\circ} $ 角,路灯采用圆锥形灯罩,灯罩的轴线 $ DO $ 与灯臂 $ CD $ 垂直,灯柱 $ BC $ 与路面 $ AB $ 垂直,此时 $ O $ 恰好为 $ AB $ 中点。
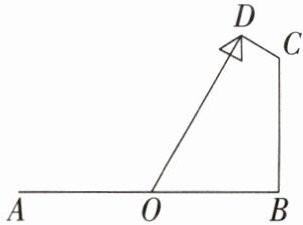
(1) $ \angle DOB $ 的度数为______ $ ^{\circ} $;
(2)现在由于道路两边都要装路灯,要求 $ OB = \frac{1}{4}AB $,且灯臂 $ CD $ 缩短为 $ 1\mathrm{m} $,其他位置关系不变,则现在路灯的灯柱 $ BC $ 高度比原设计高度缩短了______ $ \mathrm{m} $。
(1)
(2)

(1) $ \angle DOB $ 的度数为______ $ ^{\circ} $;
(2)现在由于道路两边都要装路灯,要求 $ OB = \frac{1}{4}AB $,且灯臂 $ CD $ 缩短为 $ 1\mathrm{m} $,其他位置关系不变,则现在路灯的灯柱 $ BC $ 高度比原设计高度缩短了______ $ \mathrm{m} $。
(1)
60
(2)
6√3−6
答案:
(1)60
(2)(6√3−6)[提示:
(1)
∵OD⊥DC,BC⊥AB,
∴∠ODC=∠ABC=90°.
∵∠DCB=120°,
∴∠DOB=360°−∠ODC−∠DCB−∠ABC=60°.
(2)如图,延长OD,BC 交于点E,在Rt△OBE中,∠E=90°−∠EOB=90°−60°=30°,当DC=4m时,点O为AB的中点,
∴OB=1/2AB=1/2×24=12(m),
∴OE=2OB=24(m),
∴BE=√(OE²−OB²)=√(24²−12²)=12√3(m).在Rt△DCE中,∠EDC=90°,CE=2DC=2×4=8(m),
∴BC=BE−CE=(12√3−8)m.当DC=1m时,在Rt△DCE中,∠EDC=90°,
∴CE=2DC=2×1=2(m).
∵AB=24m,OB=1/4AB,
∴OB=1/4×24=6(m),
∴OE=2OB=2×6=12(m),
∴BE=√(OE²−OB²)=√(12²−6²)=6√3(m),
∴BC=BE−CE=(6√3−2)m,
∴BC高度比原设计高度缩短了(12√3−8)−(6√3−2)=(6√3−6)(m).]
(1)60
(2)(6√3−6)[提示:
(1)
∵OD⊥DC,BC⊥AB,
∴∠ODC=∠ABC=90°.
∵∠DCB=120°,
∴∠DOB=360°−∠ODC−∠DCB−∠ABC=60°.
(2)如图,延长OD,BC 交于点E,在Rt△OBE中,∠E=90°−∠EOB=90°−60°=30°,当DC=4m时,点O为AB的中点,
∴OB=1/2AB=1/2×24=12(m),
∴OE=2OB=24(m),
∴BE=√(OE²−OB²)=√(24²−12²)=12√3(m).在Rt△DCE中,∠EDC=90°,CE=2DC=2×4=8(m),
∴BC=BE−CE=(12√3−8)m.当DC=1m时,在Rt△DCE中,∠EDC=90°,
∴CE=2DC=2×1=2(m).
∵AB=24m,OB=1/4AB,
∴OB=1/4×24=6(m),
∴OE=2OB=2×6=12(m),
∴BE=√(OE²−OB²)=√(12²−6²)=6√3(m),
∴BC=BE−CE=(6√3−2)m,
∴BC高度比原设计高度缩短了(12√3−8)−(6√3−2)=(6√3−6)(m).]
8. 如图①是一个简易手机支架,由水平底板 $ DE $,侧支撑杆 $ BD $ 和手机托盘 $ AC $ 组成,侧面示意图如图②所示。已知手机托盘 $ AC = 10\mathrm{cm} $,侧支撑杆 $ BD = 10\mathrm{cm} $, $ \angle CBD = 75^{\circ} $, $ \angle BDE = 60^{\circ} $,其中点 $ A $ 为手机托盘最高点,支撑点 $ B $ 是 $ AC $ 的中点,手机托盘 $ AC $ 可绕点 $ B $ 转动,侧支撑杆 $ BD $ 可绕点 $ D $ 转动。(参考数据: $ \tan 26.6^{\circ} \approx 0.5 $, $ \sqrt{2} \approx 1.41 $, $ \sqrt{3} \approx 1.73 $)
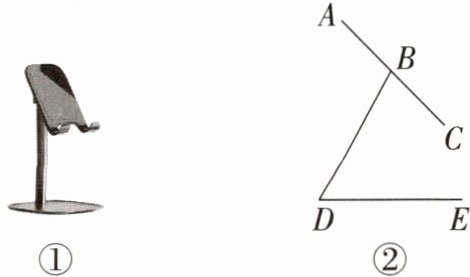
(1)如图②,求手机托盘最高点 $ A $ 离水平底板 $ DE $ 的高度 $ h $;(结果精确到 $ 0.1\mathrm{cm} $)
(2)在图②的情况下,把手机托盘 $ AC $ 绕点 $ B $ 逆时针旋转 $ 15^{\circ} $ 后,再将 $ BD $ 绕点 $ D $ 顺时针旋转 $ \alpha $,使点 $ C $ 落在直线 $ DE $ 上,求 $ \alpha $。(结果精确到 $ 0.1^{\circ} $)

(1)如图②,求手机托盘最高点 $ A $ 离水平底板 $ DE $ 的高度 $ h $;(结果精确到 $ 0.1\mathrm{cm} $)
(2)在图②的情况下,把手机托盘 $ AC $ 绕点 $ B $ 逆时针旋转 $ 15^{\circ} $ 后,再将 $ BD $ 绕点 $ D $ 顺时针旋转 $ \alpha $,使点 $ C $ 落在直线 $ DE $ 上,求 $ \alpha $。(结果精确到 $ 0.1^{\circ} $)
答案:
(1)如图①,作BF⊥DE于点F,BG//DE,AG⊥BG于点G,
∵∠BDE=60°,
∴∠DBF=30°.又
∵BD=10cm,
∴BF=5√3cm.
∵∠CBD=75°,
∴∠CBF=45°,
∴∠ABG=45°.
∵AC=10cm,B是AC的中点,
∴AB=5cm,
∴AG=5√2/2,
∴h=AG+BF=5√2/2+5√3≈12.2(cm).
(2)如图②,由条件,得∠DBC=90°,又
∵BD=10cm,BC=5cm,
∴tan∠BDC=BC/BD=0.5,
∴∠BDC≈26.6°,
∴α≈60°-26.6°=33.4°.
(1)如图①,作BF⊥DE于点F,BG//DE,AG⊥BG于点G,
∵∠BDE=60°,
∴∠DBF=30°.又
∵BD=10cm,
∴BF=5√3cm.
∵∠CBD=75°,
∴∠CBF=45°,
∴∠ABG=45°.
∵AC=10cm,B是AC的中点,
∴AB=5cm,
∴AG=5√2/2,
∴h=AG+BF=5√2/2+5√3≈12.2(cm).
(2)如图②,由条件,得∠DBC=90°,又
∵BD=10cm,BC=5cm,
∴tan∠BDC=BC/BD=0.5,
∴∠BDC≈26.6°,
∴α≈60°-26.6°=33.4°.
9. 消防车是救援火灾的重要装备。图①是一辆登高云梯消防车的实物图,图②是其工作示意图,起重臂 $ AB $ 可伸缩,伸缩范围为 $ 10\mathrm{m} \leq AB \leq 40\mathrm{m} $,且起重臂 $ AB $ 可绕点 $ A $ 在一定范围内转动,张角为 $ \angle CAB $,张角范围为 $ 90^{\circ} \leq \angle CAB \leq 150^{\circ} $,转动点 $ A $ 距离地面 $ MN $ 的高度 $ AC $ 为 $ 5\mathrm{m} $。(参考数据: $ \cos 32^{\circ} \approx 0.85 $, $ \sin 32^{\circ} \approx 0.53 $)
 (1)当起重臂 $ AB $ 长度为 $ 20\mathrm{m} $,张角为 $ 135^{\circ} $ 时,求云梯消防车最高点 $ B $ 距地面的高度。(结果保留根号)
(1)当起重臂 $ AB $ 长度为 $ 20\mathrm{m} $,张角为 $ 135^{\circ} $ 时,求云梯消防车最高点 $ B $ 距地面的高度。(结果保留根号)
(2)某栋楼高 $ 39\mathrm{m} $,若该楼中有居民家突发险情,则该消防车能否实施有效救援?请说明理由。
 (1)当起重臂 $ AB $ 长度为 $ 20\mathrm{m} $,张角为 $ 135^{\circ} $ 时,求云梯消防车最高点 $ B $ 距地面的高度。(结果保留根号)
(1)当起重臂 $ AB $ 长度为 $ 20\mathrm{m} $,张角为 $ 135^{\circ} $ 时,求云梯消防车最高点 $ B $ 距地面的高度。(结果保留根号)(2)某栋楼高 $ 39\mathrm{m} $,若该楼中有居民家突发险情,则该消防车能否实施有效救援?请说明理由。
答案:
(1)如图,过点B作BD⊥AD,交CA的延长线于点D,过点B作BE⊥MN,垂足为E.
∵BD⊥AD,BE⊥MN,DC⊥MN,
∴四边形DBEC是矩形.
∴BE=DC.由题意,知∠CAB=135°,
∴∠DAB=45°.在Rt△ADB中,
∵cos∠DAB=AD/AB,
∴AD=AB·cos∠DAB=20×cos45°=20×√2/2=10√2,
∴CD=AC+AD=5+10√2.
∴BE=5+10√2.故当起重臂AB长度为20m,张角为135°时,云梯消防车最高点B距地面的高度为(5+10√2)m.
(2)该消防车能实施有效救援.理由如下:当BE=39m时,
∵AC=5m,
∴AD=34m.在Rt△ADB中,当AB=40m时,
∵cos∠DAB=AD/AB=34/40=0.85,
∴∠DAB≈32°.
∴∠CAB=148°.
∵张角∠CAB范围为90°≤∠CAB≤150°,
∴该消防车能实施有效救援.
(1)如图,过点B作BD⊥AD,交CA的延长线于点D,过点B作BE⊥MN,垂足为E.
∵BD⊥AD,BE⊥MN,DC⊥MN,
∴四边形DBEC是矩形.
∴BE=DC.由题意,知∠CAB=135°,
∴∠DAB=45°.在Rt△ADB中,
∵cos∠DAB=AD/AB,
∴AD=AB·cos∠DAB=20×cos45°=20×√2/2=10√2,
∴CD=AC+AD=5+10√2.
∴BE=5+10√2.故当起重臂AB长度为20m,张角为135°时,云梯消防车最高点B距地面的高度为(5+10√2)m.
(2)该消防车能实施有效救援.理由如下:当BE=39m时,
∵AC=5m,
∴AD=34m.在Rt△ADB中,当AB=40m时,
∵cos∠DAB=AD/AB=34/40=0.85,
∴∠DAB≈32°.
∴∠CAB=148°.
∵张角∠CAB范围为90°≤∠CAB≤150°,
∴该消防车能实施有效救援.
查看更多完整答案,请扫码查看


