第22页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
7. 如图,在平面直角坐标系中,△ABC与△A'B'C'是位似图形,位似中心是原点O,若A(2,a),A'(4,b),则△ABC与△A'B'C'的相似比是(

A.1:2
B.2:3
C.1:4
D.1:3
A
)
A.1:2
B.2:3
C.1:4
D.1:3
答案:
A
8. 如图,平面直角坐标系中,△ABC与△FED关于原点O位似,OB= 2OE,若四边形AOCB的面积为4,则四边形FODE的面积为(
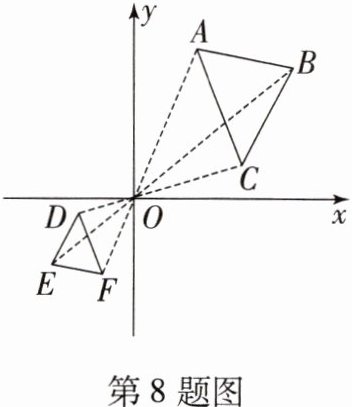
A.1/2
B.1
C.3/2
D.2
1
)
A.1/2
B.1
C.3/2
D.2
答案:
B[提示:由题意知△ABC与△FED的相似比为2:1.$\frac{OB}{OE}=\frac{OA}{OF}$,∠AOB=∠FOE,
∴△AOB与△FOE相似,且相似比为2:1,同理,△COB与△DOE相似,且相似比为2:1.
∵$S_{四边形AOCB}=S_{\triangle AOB}+S_{\triangle BCO}$,$S_{四边形FODE}=S_{\triangle FOE}+S_{\triangle EDO}$,
∴四边形AOCB与四边形FODE的相似比为2:1,
∴四边形AOCB与四边形FODE的面积比为4:1.
∵四边形AOCB的面积为4,
∴四边形FODE的面积为1.]
∴△AOB与△FOE相似,且相似比为2:1,同理,△COB与△DOE相似,且相似比为2:1.
∵$S_{四边形AOCB}=S_{\triangle AOB}+S_{\triangle BCO}$,$S_{四边形FODE}=S_{\triangle FOE}+S_{\triangle EDO}$,
∴四边形AOCB与四边形FODE的相似比为2:1,
∴四边形AOCB与四边形FODE的面积比为4:1.
∵四边形AOCB的面积为4,
∴四边形FODE的面积为1.]
9. 如图,在平面直角坐标系中,△ABC的顶点坐标分别是A(-1,1),B(-2,0),C(0,-2)。
(1)以原点O为位似中心,在点O另一侧画△A'B'C',使它与△ABC位似,且相似比为2:1;
(2)若四边形AA'B'P是矩形,则点P的坐标为______。
]
(1)
(2)
(1)以原点O为位似中心,在点O另一侧画△A'B'C',使它与△ABC位似,且相似比为2:1;
(2)若四边形AA'B'P是矩形,则点P的坐标为______。
]

(1)
如图,△A'B'C'即为所求.
(2)
(1,3)
答案:
解:
(1)如图,△A'B'C'即为所求.
(2)
∵A(-1,1),B(-2,0),△A'B'C'与△ABC位似,相似比为2:1,且图形在原点两旁,
∴A'(2,-2),B'(4,0).由四边形AA'B'P是矩形及平移的性质,可得P(1,3).
(1)如图,△A'B'C'即为所求.
(2)
∵A(-1,1),B(-2,0),△A'B'C'与△ABC位似,相似比为2:1,且图形在原点两旁,
∴A'(2,-2),B'(4,0).由四边形AA'B'P是矩形及平移的性质,可得P(1,3).
10. (2023·烟台海阳市期末)如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-3,2),B(-1,3),C(-1,1)。
(1)以点O为位似中心,在x轴下方,画出△ABC的位似图形$△A_1B_1C_1,$使它与△ABC的相似比为2:1;
(2)若△ABC内部一点M的坐标为(a,b),请直接写出点M在$△A_1B_1C_1$中的对应点$M_1$的坐标。
]
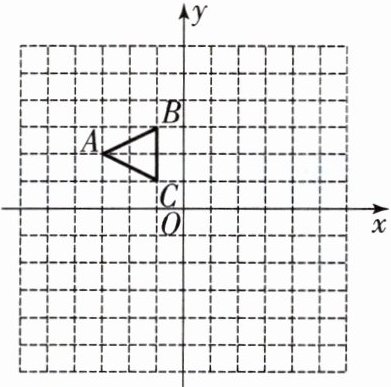
(1)以点O为位似中心,在x轴下方,画出△ABC的位似图形$△A_1B_1C_1,$使它与△ABC的相似比为2:1;
(2)若△ABC内部一点M的坐标为(a,b),请直接写出点M在$△A_1B_1C_1$中的对应点$M_1$的坐标。
]

答案:
解:
(1)如图,△A₁B₁C₁即为所求.
(2)
∵△A₁B₁C₁与△ABC是以原点O为位似中心的位似图形,M(a,b)是△ABC内部一点,
∴点M在△A₁B₁C₁中的对应点M₁的坐标为(-2a,-2b).
(1)如图,△A₁B₁C₁即为所求.
(2)
∵△A₁B₁C₁与△ABC是以原点O为位似中心的位似图形,M(a,b)是△ABC内部一点,
∴点M在△A₁B₁C₁中的对应点M₁的坐标为(-2a,-2b).
11. (2023·淄博桓台县期末)如图,已知点O是坐标原点,网格中小正方形的边长为1,B(2,2)。
(1)
(2)
]
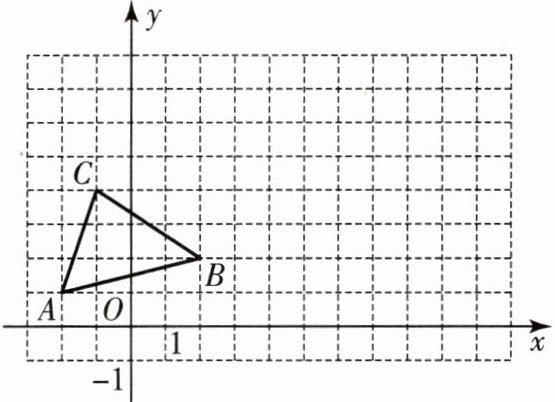
(1)
(画图略,根据位似中心A及相似比2:1在x轴上方画出△AB'C')
以点A为位似中心,在x轴的上方将△ABC放大到原图的2倍(即新图与原图的相似比为2:1),画出对应的△AB'C';(2)
$\frac{33}{2}$
四边形CBB'C'的面积为______。]

答案:
解:
(1)如图,△AB'C'即为所求.
(2)$S_{四边形CBB'C'}=5× 7-\frac{1}{2}× 1× 3-\frac{1}{2}× 6× 4-\frac{1}{2}× 2× 3-\frac{1}{2}× 1× 4=\frac{33}{2}$.
(1)如图,△AB'C'即为所求.
(2)$S_{四边形CBB'C'}=5× 7-\frac{1}{2}× 1× 3-\frac{1}{2}× 6× 4-\frac{1}{2}× 2× 3-\frac{1}{2}× 1× 4=\frac{33}{2}$.
12. (2023·威海荣成市期末)如图,在边长为1的小正方形组成的网格中,△ABC的顶点在格点(网格线的交点)上,以点O为原点建立平面直角坐标系,点B的坐标为(1,0)。
(1)将△ABC向左平移5个单位长度,得到$△A_1B_1C_1,$画出$△A_1B_1C_1;$
(2)以点O为位似中心,在x轴下方将$△A_1B_1C_1$放大到原图的2倍(即新图与原图的相似比为2:1),得到$△A_2B_2C_2,$在所给的网络中画出$△A_2B_2C_2;$
(3)若点M是AB的中点,经过(1),(2)两次变换,M的对应点$M_2$的坐标是
]
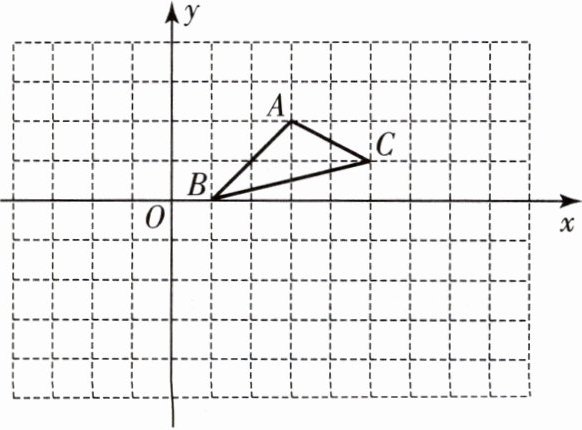
(1)将△ABC向左平移5个单位长度,得到$△A_1B_1C_1,$画出$△A_1B_1C_1;$
(2)以点O为位似中心,在x轴下方将$△A_1B_1C_1$放大到原图的2倍(即新图与原图的相似比为2:1),得到$△A_2B_2C_2,$在所给的网络中画出$△A_2B_2C_2;$
(3)若点M是AB的中点,经过(1),(2)两次变换,M的对应点$M_2$的坐标是
(6,-2)
。]

答案:
解:
(1)如图,△A₁B₁C₁即为所求.
(2)如图,△A₂B₂C₂即为所求.
(3)若点M是AB的中点,经过
(1),
(2)两次变换,M的对应点M₂的坐标为(6,-2).
(1)如图,△A₁B₁C₁即为所求.
(2)如图,△A₂B₂C₂即为所求.
(3)若点M是AB的中点,经过
(1),
(2)两次变换,M的对应点M₂的坐标为(6,-2).
查看更多完整答案,请扫码查看


