第13页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. 如图,在同一时刻,身高1.6m的小丽在阳光下的影长为2.5m,一棵大树的影长为5m,则这棵树的高度为(

A.1.5m
B.2.3m
C.3.2m
D.7.8m
C
)
A.1.5m
B.2.3m
C.3.2m
D.7.8m
答案:
C
2. 如图,身高为1.5米的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC= 3米,CA= 1米,则树的高度为(

A.3米
B.4米
C.4.5米
D.6米
D
)
A.3米
B.4米
C.4.5米
D.6米
答案:
D[提示:由题意,得△ACD∽△ABE,
∴$\frac{CD}{BE}$=$\frac{CA}{AB}$,即$\frac{1.5}{BE}$=$\frac{1}{1+3}$,解得BE=6,即树的高度为6米.]
∴$\frac{CD}{BE}$=$\frac{CA}{AB}$,即$\frac{1.5}{BE}$=$\frac{1}{1+3}$,解得BE=6,即树的高度为6米.]
3. 如图,淇淇同学在湖边看湖对面的一棵树,他目测自己与树的距离为20m,树的顶端在水中的倒影距自己5m远,淇淇的眼睛离地面的高度为1.7m,则树高为(
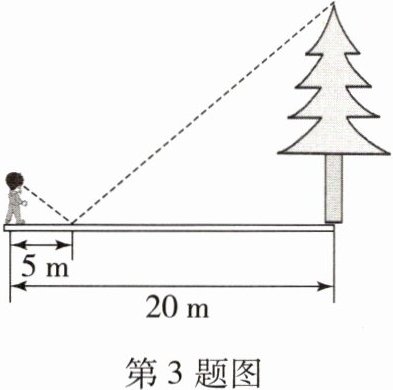
A.3.4m
B.4.7m
C.5.1m
D.6.8m
C
)
A.3.4m
B.4.7m
C.5.1m
D.6.8m
答案:
C
4. (2023·四川南充中考)如图,数学活动课上,为测量学校旗杆高度,小菲同学在脚下水平放置一平面镜(平面镜的大小、厚度忽略不计),然后向后退(保持脚、镜子和旗杆底端在同一直线上),直到她刚好在镜子中看到旗杆的顶端.已知小菲的眼睛离地面高度为1.6m,同时量得小菲与镜子的水平距离为2m,镜子与旗杆的水平距离为10m,则旗杆高度为(

A.6.4m
B.8m
C.9.6m
D.12.5m
B
)
A.6.4m
B.8m
C.9.6m
D.12.5m
答案:
B[提示:如图,
∵AB⊥BD,DE⊥BD,
∴∠ABC=∠EDC=90°.
∵∠ACB=∠ECD,
∴△ABC∽△EDC,
∴$\frac{AB}{DE}$=$\frac{BC}{CD}$,即$\frac{1.6}{DE}$=$\frac{2}{10}$
∴DE=8(m).]
∵AB⊥BD,DE⊥BD,
∴∠ABC=∠EDC=90°.
∵∠ACB=∠ECD,
∴△ABC∽△EDC,
∴$\frac{AB}{DE}$=$\frac{BC}{CD}$,即$\frac{1.6}{DE}$=$\frac{2}{10}$
∴DE=8(m).]
5. (2023·潍坊中考)在《数书九章》(宋·秦九韶)中记载了一个测量塔高的问题:如图,AB表示塔的高度,CD表示竹竿顶端到地面的高度,EF表示人眼到地面的高度,AB,CD,EF在同一平面内,点A,C,E在一条水平直线上.已知AC= 20m,CE= 10m,CD= 7m,EF= 1.4m,人从点F远眺塔顶B,视线恰好经过竹竿的顶端D,可求出塔的高度.根据以上信息,塔的高度为

18.2
m.
答案:
18.2[提示:如图,过点F作FG⊥CD,垂足为G,延长FG交AB于点H,由题意得FH⊥AB,AH=CG=EF=1.4,AC=GH =20,CE=FG=10,
∴∠DGF=∠BHF=90°.
∵CD=7,
∴DG=CD−CG=7−1.4=5.6.
∵∠DFG=∠BFH,
∴△FDG∽△FBH,
∴$\frac{DG}{BH}$=$\frac{FG}{FH}$,
∴$\frac{5.6}{BH}$=$\frac{10}{10+20}$,
∴BH=16.8,
∴AB=BH+AH=16.8+1.4=18.2(m),
∴塔的高度为18.2m.]
∴∠DGF=∠BHF=90°.
∵CD=7,
∴DG=CD−CG=7−1.4=5.6.
∵∠DFG=∠BFH,
∴△FDG∽△FBH,
∴$\frac{DG}{BH}$=$\frac{FG}{FH}$,
∴$\frac{5.6}{BH}$=$\frac{10}{10+20}$,
∴BH=16.8,
∴AB=BH+AH=16.8+1.4=18.2(m),
∴塔的高度为18.2m.]
6. 如图①,滹(hū)沱河是山西地区一条途经了舟山和太行山的知名河流,这条河流的流域面积达到了2.73万平方公里,其发源于山西省繁峙县泰戏山桥儿沟村一带,这条河流早在《山海经》中就有出现过,被叫做滹池.为了估算河流的宽度,在所在的河岸边取点A和C,河对岸选定一个目标P,使点P,A,C共线且与河垂直,接着在过点C且与直线PC垂直的直线上选择适当的点D,确定PD与过点A且与PC垂直的直线的交点B(示意图如图②),测得AC= 50m,CD= 120m,AB= 80m,请根据这些数据求河的宽度PA.
]

]

答案:
解:由题意得AB⊥PC,CD⊥PC,AC=50m,CD=120m,AB =80m,
∵AB//CD,
∴∠PAB=∠PCD,∠PBA=∠PDC,
∴△PAB∽△PCD,
∴$\frac{PA}{PC}$=$\frac{AB}{CD}$,即$\frac{PA}{PA+AC}$=$\frac{AB}{CD}$,
∴$\frac{PA}{PA+50}$=$\frac{80}{120}$,解得PA=100(m).
∵AB//CD,
∴∠PAB=∠PCD,∠PBA=∠PDC,
∴△PAB∽△PCD,
∴$\frac{PA}{PC}$=$\frac{AB}{CD}$,即$\frac{PA}{PA+AC}$=$\frac{AB}{CD}$,
∴$\frac{PA}{PA+50}$=$\frac{80}{120}$,解得PA=100(m).
查看更多完整答案,请扫码查看


