《2025年全科王同步课时练习九年级数学上册青岛版》

8. (2023·山东泰安中考)如图,在平面直角坐标系中,△AOB为等边三角形,点A的坐标为(1,0).把△AOB按如图所示的方式放置,并将△AOB进行变换:第一次将△AOB绕着原点O顺时针旋转60°,同时边长扩大为△AOB边长的2倍,得到△A₁OB₁;第二次将△A₁OB₁绕着原点O顺时针旋转60°,同时边长扩大为△A₁OB₁边长的2倍,得到△A₂OB₂,…,以此类推,得到$△A_{2023}OB_{2023},则△A_{2023}OB_{2023}$的边长为2²⁰²³,点$A_{2023}$的坐标为(2²⁰²²,−2²⁰²²√3).

答案： 2²⁰²³ (2022,−2²⁰²²√3)[提示:由题意OA=1=2⁰,OA₁=2=2¹,OA₂=4=2²,OA₃=8=2³,...,OAₙ=2ⁿ,n∈N,
∴△A₂₀₂₃OB₂₀₂₃的边长为2²⁰²³.
∵2023÷6=337……1,
∴A₂₀₂₃与A₁都在第四象限,坐标为(2²⁰²²,−2²⁰²²·√3).]

9. (2023·四川乐山中考)如图,在平行四边形ABCD中,E是线段AB上一点,连接AC,DE,交于点F.若$\frac{AE}{EB}= \frac{2}{3}$,则$\frac{S_{△ADF}}{S_{△AEF}}= $$\frac{5}{2}$.

答案： $\frac{5}{2}$[提示:
∵四边形ABCD是平行四边形，
∴AB//CD,AB=CD.
∵$\frac{AE}{EB}$=$\frac{2}{3}$,
∴设AE=2a,则BE=3a,
∴CD=AB=5a.
∵AB//CD,
∴△AEF∽△CDF,
∴$\frac{AE}{CD}$=$\frac{EF}{DF}$=$\frac{2}{5}$,
∴S△ADF/S△AEF=$\frac{5}{2}$.]

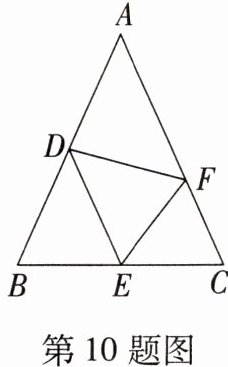
10. (2023·浙江杭州中考)如图,在△ABC中,AB= AC,∠A＜90°,点D,E,F分别在边AB,BC,CA上,连接DE,EF,FD,已知点B和点F关于直线DE对称.设$\frac{BC}{AB}= k$,若AD= DF,则$\frac{CF}{FA}= $$\frac{k²}{2−k²}$.(结果用含k的代数式表示)

答案： $\frac{k²}{2−k²}$[提示:
∵点B和点F关于直线DE对称，
∴DB=DF,∠BDE=∠FDE,∠DEB=∠DEF.
∵AD=DF,
∴AD=DB,∠A=∠DFA.
∵∠BDE+∠FDE=∠BDF=∠A+∠DFA,
∴∠FDE=∠DFA,
∴DE//AC,
∴∠C=∠DEB,∠DEF=∠EFC.
∵∠DEB=∠DEF,
∴∠C=∠EFC.
∵AB=AC,
∴∠C=∠B.
∵∠ACB=∠EFC,
∴△ABC∽△ECF,
∴$\frac{AB}{EC}$=$\frac{BC}{CF}$.
∵DE//AC,
∴∠BDE=∠A,∠BED=∠C,
∴△BDE∽△BAC,
∴$\frac{BE}{BC}$=$\frac{BD}{BA}$=$\frac{1}{2}$,
∴EC=$\frac{1}{2}$BC.
∵$\frac{BC}{AB}$=k,
∴BC=k·AB,
∴EC=$\frac{1}{2}$k·AB,
∵$\frac{AB}{EC}$=$\frac{BC}{CF}$,
∴$\frac{AB}{\frac{1}{2}k·AB}$=$\frac{k·AB}{CF}$,
∴CF=$\frac{1}{2}$k²·AB,
∴$\frac{CF}{FA}$=$\frac{CF}{AC−CF}$=$\frac{CF}{AB−CF}$=$\frac{\frac{1}{2}k²·AB}{AB−\frac{1}{2}k²·AB}$=$\frac{k²}{2−k²}$.]

11. 如图,在Rt△ABC中,∠ACB= 90°,点M在边AB上,线段MC绕点M顺时针旋转,点C恰巧落在边AC上的点N处.如果$\frac{AN}{NC}= n$,$\frac{AM}{MB}= m$,那么n与m满足的关系式是 (A)

A.m - 2n = 1
B.m - 3n = 1
C.2m - 2n = 1
D.2m - 3n = 1

答案： A[提示:过M点作MH⊥AC于H点，如图，
∵线段MC绕点M顺时针旋转，点C恰巧落在边AC上的点N处，
∴MN=MC.
∵MH⊥CN,
∴NH=CH=$\frac{1}{2}$CN,∠AHM=90°.
∵∠ACB=90°,
∴MH//BC,
∴$\frac{AM}{MB}$=$\frac{AH}{HC}$,即$\frac{AM}{MB}$=$\frac{AN+\frac{1}{2}NC}{\frac{1}{2}NC}$=$\frac{2AN}{NC}$+1.
∵$\frac{AN}{NC}$=n,$\frac{AM}{MB}$=m,
∴m=2n+1,即m−2n=1.]

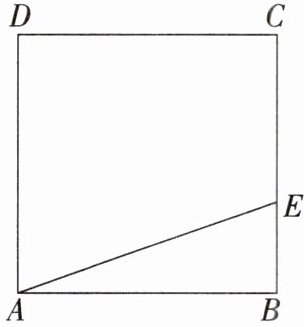
12. 如图,正方形ABCD中,点E是边BC上的一点,连接AE,将射线AE绕点A逆时针旋转90°,交CD的延长线于点F,连接EF,取EF的中点G,连接DG.
(1)依题意补全图形,写出∠ADG与∠CDG的数量关系,并证明;
(2)若DG= √2DF,写出线段BC与BE的数量关系,并证明.

答案： 解:
(1)如图,∠ADG=∠CDG.证明如下:连接AG,CG,
∵将射线AE绕点A逆时针旋转90°,
∴∠EAF=90°=∠BCD,
∵点G是EF的中点，
∴EF=2CG=2AG,
∴GA=GC,又
∵AD=CD,DG=DG,
∴△ADG≌△CDG,
∴∠ADG=∠CDG.
(2)BC=3BE.证明如下:如图，过点G作GH⊥CD于H,
∴GH//BC,
∴△FGH∽△FEC,
∴$\frac{GH}{CE}$=$\frac{FG}{EF}$=$\frac{1}{2}$=$\frac{FH}{FC}$,
∴CE=2GH,FC=2FH.
∵△ADG≌△CDG,
∴∠ADG=∠CDG=45°.
∵HG⊥CD,
∴∠CDG=∠DGH=45°,
∴DH=HG,
∴DG=√2HG=√2DH.
∵DG=√2DF,
∴DF=HG=DH,
∴CH=FH=2DH,
∴CD=3DH=3GH=BC,
∴BE=BC−CE=GH,
∴BC=3BE.