第46页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
7. 如图,学校环保社成员想测量斜坡$CD旁一棵树AB$的高度,他们先在点$C处测得树顶B的仰角为60^{\circ}$,然后在坡顶$D测得树顶B的仰角为30^{\circ}$,已知斜坡$CD的长度为20m$,$DE的长为10m$,则树$AB$的高度是(

A.$20\sqrt{3}m$
B.$30m$
C.$30\sqrt{3}m$
D.$40m$
B
)
A.$20\sqrt{3}m$
B.$30m$
C.$30\sqrt{3}m$
D.$40m$
答案:
B[提示:在Rt△CDE中,
∵CD=20m,DE=10m,
∴sin∠DCE=$\frac{10}{20}$=$\frac{1}{2}$,
∴∠DCE=30°.
∵∠ACB=60°,DF//AE,
∴∠BGF=60°,
∴∠ABC=30°,∠DCB=90°.
∵∠BDF=30°,
∴∠DBF=60°,
∴∠DBC=30°,
∴BC=$\frac{CD}{\tan30^{\circ}}$=$\frac{20}{\frac{\sqrt{3}}{3}}$=20$\sqrt{3}$(m),
∴AB=BC·sin60°=20$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=30(m).]
∵CD=20m,DE=10m,
∴sin∠DCE=$\frac{10}{20}$=$\frac{1}{2}$,
∴∠DCE=30°.
∵∠ACB=60°,DF//AE,
∴∠BGF=60°,
∴∠ABC=30°,∠DCB=90°.
∵∠BDF=30°,
∴∠DBF=60°,
∴∠DBC=30°,
∴BC=$\frac{CD}{\tan30^{\circ}}$=$\frac{20}{\frac{\sqrt{3}}{3}}$=20$\sqrt{3}$(m),
∴AB=BC·sin60°=20$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=30(m).]
8. 观光塔是潍坊市区的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端$A处观测观光塔顶端C处的仰角是60^{\circ}$,然后爬到该楼房顶端$B处观测观光塔底部D处的俯角是30^{\circ}$.已知楼房高$AB约是45m$,根据以上观测数据可知观光塔的高$CD$是

135m
.
答案:
135m[提示:
∵爬到该楼顶端B处观测观光塔底部D处的俯角是30°,
∴∠ADB=30°.在Rt△ABD中,tan30°=$\frac{AB}{AD}$,$\frac{45}{AD}$=$\frac{\sqrt{3}}{3}$,
∴AD=45$\sqrt{3}$m.
∵在楼房的底端A处观测观光塔顶端C处的仰角是60°,
∴在Rt△ACD中,CD=AD·tan60°=45$\sqrt{3}$×$\sqrt{3}$=135(m).]
∵爬到该楼顶端B处观测观光塔底部D处的俯角是30°,
∴∠ADB=30°.在Rt△ABD中,tan30°=$\frac{AB}{AD}$,$\frac{45}{AD}$=$\frac{\sqrt{3}}{3}$,
∴AD=45$\sqrt{3}$m.
∵在楼房的底端A处观测观光塔顶端C处的仰角是60°,
∴在Rt△ACD中,CD=AD·tan60°=45$\sqrt{3}$×$\sqrt{3}$=135(m).]
9. 如图,小莹在数学综合实践活动中,利用所学的数学知识对某小区居民楼$AB$的高度进行测量,先测得居民楼$AB与CD之间的距离AC为35m$,再站在$M点处测得居民楼CD的顶端D的仰角为45^{\circ}$,居民楼$AB的顶端B的仰角为55^{\circ}$,已知居民楼$CD的高度为16.6m$,小莹的观测点$N距地面1.6m$.求居民楼$AB$的高度.(结果精确到$1m$.参考数据:$\sin55^{\circ}\approx0.82$,$\cos55^{\circ}\approx0.57$,$\tan55^{\circ}\approx1.43$)


答案:
解:如图,过点N作EF//AC交AB于点E,交CD于点F,则AE=MN=CF=1.6m,EF=AC=35m,∠BEN=∠DFN=90°,EN=AM,NF=MC,
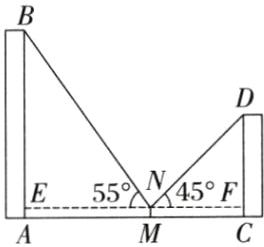
则DF=DC - CF=16.6 - 1.6 = 15(m).在Rt△DFN中,
∵∠DNF=45°,
∴NF=DF=15m,
∴EN=EF - NF=35 - 15 = 20(m).在Rt△BEN中,
∵tan∠BNE=$\frac{BE}{EN}$,
∴BE=EN·tan∠BNE=20×tan55°≈20×1.43≈28.6(m),
∴AB=BE + AE≈28.6 + 1.6≈30(m).
∴居民楼AB的高度约为30m.
解:如图,过点N作EF//AC交AB于点E,交CD于点F,则AE=MN=CF=1.6m,EF=AC=35m,∠BEN=∠DFN=90°,EN=AM,NF=MC,

则DF=DC - CF=16.6 - 1.6 = 15(m).在Rt△DFN中,
∵∠DNF=45°,
∴NF=DF=15m,
∴EN=EF - NF=35 - 15 = 20(m).在Rt△BEN中,
∵tan∠BNE=$\frac{BE}{EN}$,
∴BE=EN·tan∠BNE=20×tan55°≈20×1.43≈28.6(m),
∴AB=BE + AE≈28.6 + 1.6≈30(m).
∴居民楼AB的高度约为30m.
10. (2023·潍坊昌乐县月考)如图,要测量铁塔的高$AB$,在地面上选取一点$C$,在$A$,$C两点间选取一点D$,测得$CD = 14m$,在$C$,$D两点处分别用测角仪测得铁塔顶端B的仰角\alpha = 30^{\circ}和\beta = 45^{\circ}$.测角仪支架的高$CC_{1}为1.2m$,求铁塔的高.(结果精确到$0.1m$.参考数据:$\sqrt{3}\approx1.73$)


答案:
解:由题意得AA₁=DD₁=CC₁=1.2,CD=C₁D₁=14,∠BD₁A₁=45°,∠BC₁A₁=30°.设A₁B=x,在Rt△BA₁D₁中,∠BD₁A₁=45°,
∴A₁B=A₁D₁=x,
∴A₁C₁=A₁D₁+D₁C₁=x + 14.在Rt△BA₁C₁中,tan30°=$\frac{A₁B}{A₁C₁}$=$\frac{x}{x+14}$=$\frac{\sqrt{3}}{3}$,解得x=7($\sqrt{3}$+1),
∴AB=A₁B+A₁A=7($\sqrt{3}$+1)+1.2≈20.3(m),
∴铁塔的高约为20.3m.
∴A₁B=A₁D₁=x,
∴A₁C₁=A₁D₁+D₁C₁=x + 14.在Rt△BA₁C₁中,tan30°=$\frac{A₁B}{A₁C₁}$=$\frac{x}{x+14}$=$\frac{\sqrt{3}}{3}$,解得x=7($\sqrt{3}$+1),
∴AB=A₁B+A₁A=7($\sqrt{3}$+1)+1.2≈20.3(m),
∴铁塔的高约为20.3m.
11. (2023·烟台莱州期中)无人机在实际生活中应用广泛,如图,小明利用无人机测量大楼的高度,无人机在空中$P$处,测得楼$CD楼顶D处的俯角为45^{\circ}$,测得楼$AB楼顶A处的俯角为60^{\circ}$,已知楼$AB和楼CD之间的距离BC为100\sqrt{3}m$,楼$AB的高度为10m$,从楼$AB的A处测得楼CD楼顶D处的仰角为30^{\circ}$.(点$A$,$B$,$C$,$D$,$P$在同一平面内,参考数据:$\sqrt{3}\approx1.732$,$\sqrt{2}\approx1.414$)
(1) 填空:$\angle ADP= $
(2) 求楼$CD$的高度;
(3) 求此时无人机距离地面$BC$的高度.(结果精确到$1m$)

(1) 填空:$\angle ADP= $
75
$^{\circ}$;(2) 求楼$CD$的高度;
(2)解:由题意可得AE=BC=100$\sqrt{3}$m,EC=AB=10m,在Rt△AED中,∠DAE=30°,tan30°=$\frac{DE}{AE}$=$\frac{DE}{100\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,解得DE=100m,
∴CD=DE + EC=100 + 10 = 110(m).
∴楼CD的高度为110m;
∴CD=DE + EC=100 + 10 = 110(m).
∴楼CD的高度为110m;
(3) 求此时无人机距离地面$BC$的高度.(结果精确到$1m$)
(3)解:如图②,过点P作PG⊥BC于点G,交AE于点F,则∠PFA=∠AED=90°,FG=AB=10m.
∵MN//AE,
∴∠PAF=∠MPA=60°.
∵∠ADE=60°,
∴∠PAF=∠ADE.由
(1)知∠APD=75°,∠ADP=75°,
∴∠ADP=∠APD,则AP=AD,
∴△APF≌△DAE,
∴PF=AE=100$\sqrt{3}$m,
∴PG=PF+FG=(100$\sqrt{3}$+10)(m).
∴此时无人机距离地面BC的高度为(100$\sqrt{3}$+10)m.
∵MN//AE,
∴∠PAF=∠MPA=60°.
∵∠ADE=60°,
∴∠PAF=∠ADE.由
(1)知∠APD=75°,∠ADP=75°,
∴∠ADP=∠APD,则AP=AD,
∴△APF≌△DAE,
∴PF=AE=100$\sqrt{3}$m,
∴PG=PF+FG=(100$\sqrt{3}$+10)(m).
∴此时无人机距离地面BC的高度为(100$\sqrt{3}$+10)m.

答案:
(1)75;
(2)解:由题意可得AE=BC=100$\sqrt{3}$m,EC=AB=10m,在Rt△AED中,∠DAE=30°,tan30°=$\frac{DE}{AE}$=$\frac{DE}{100\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,解得DE=100m,
∴CD=DE + EC=100 + 10 = 110(m).
∴楼CD的高度为110m;
(3)解:如图②,过点P作PG⊥BC于点G,交AE于点F,则∠PFA=∠AED=90°,FG=AB=10m.
∵MN//AE,
∴∠PAF=∠MPA=60°.
∵∠ADE=60°,
∴∠PAF=∠ADE.由
(1)知∠APD=75°,∠ADP=75°,
∴∠ADP=∠APD,则AP=AD,
∴△APF≌△DAE,
∴PF=AE=100$\sqrt{3}$m,
∴PG=PF+FG=(100$\sqrt{3}$+10)(m).
∴此时无人机距离地面BC的高度为(100$\sqrt{3}$+10)m.
(1)75;
(2)解:由题意可得AE=BC=100$\sqrt{3}$m,EC=AB=10m,在Rt△AED中,∠DAE=30°,tan30°=$\frac{DE}{AE}$=$\frac{DE}{100\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,解得DE=100m,
∴CD=DE + EC=100 + 10 = 110(m).
∴楼CD的高度为110m;
(3)解:如图②,过点P作PG⊥BC于点G,交AE于点F,则∠PFA=∠AED=90°,FG=AB=10m.
∵MN//AE,
∴∠PAF=∠MPA=60°.
∵∠ADE=60°,
∴∠PAF=∠ADE.由
(1)知∠APD=75°,∠ADP=75°,
∴∠ADP=∠APD,则AP=AD,
∴△APF≌△DAE,
∴PF=AE=100$\sqrt{3}$m,
∴PG=PF+FG=(100$\sqrt{3}$+10)(m).
∴此时无人机距离地面BC的高度为(100$\sqrt{3}$+10)m.
查看更多完整答案,请扫码查看


