《2025年全科王同步课时练习九年级数学上册青岛版》

15. 已知$\alpha$是锐角,$2\cos (\alpha +45^{\circ})= 1$,则$\alpha$的值是(A)
A.$15^{\circ}$
B.$30^{\circ}$
C.$45^{\circ}$
D.$60^{\circ}$

答案： A[提示:
∵2$\cos(\alpha + 45°)$ = 1,
∴$\cos(\alpha + 45°) = \frac{1}{2}$.又
∵$\cos60° = \frac{1}{2}$,
∴$\alpha + 45° = 60°$,解得$\alpha = 15°$.]

16. 如图,钓鱼时不变形的钓鱼竿$AC长6m$,露在水面上的鱼线$BC长3\sqrt{2}m$,某钓者想看看钓钩上的情况,把鱼竿$AC转动到AC'$的位置,此时露在水面上的鱼线$B'C'长3\sqrt{3}m$,则鱼竿转过的角度是(C)

A.$60^{\circ}$
B.$45^{\circ}$
C.$15^{\circ}$
D.$90^{\circ}$

答案： C[提示:
∵$\sin\angle CAB = \frac{BC}{AC} = \frac{3\sqrt{2}}{6} = \frac{\sqrt{2}}{2}$,
∴∠CAB = 45°.
∵$\sin\angle C'AB' = \frac{B'C'}{AC'} = \frac{3\sqrt{3}}{6} = \frac{\sqrt{3}}{2}$,
∴∠C'AB' = 60°.
∴∠CAC' = 60° - 45° = 15°,故鱼竿转过的角度是15°.]

17. 已知$\alpha$为锐角,当$\dfrac{1}{1-\tan \alpha }$无意义时,$\sin (\alpha +15^{\circ})+\cos (\alpha -15^{\circ})$的值为(A)
A.$\sqrt{3}$
B.$\dfrac{\sqrt{3}}{2}$
C.$\dfrac{\sqrt{3}}{3}$
D.$\dfrac{2\sqrt{3}}{3}$

答案： A[提示:
∵$\frac{1}{1 - \tan\alpha}$无意义,
∴1 - $\tan\alpha$ = 0,即$\tan\alpha = 1$,
∴锐角$\alpha = 45°$.
∴$\sin(\alpha + 15°) + \cos(\alpha - 15°) = \sin60° + \cos30° = \frac{\sqrt{3}}{2} + \frac{\sqrt{3}}{2} = \sqrt{3}$.]

18. 若$\alpha$,$\beta$为某直角三角形的两个锐角,$\cos \alpha = \dfrac{5}{9}$,求$\sin \beta$的值。

答案： 解:
∵$\alpha$,$\beta$为某直角三角形的两个锐角,
∴$\sin\beta = \cos(90° - \beta) = \cos\alpha = \frac{5}{9}$.

19. 如图,在正方形$ABCD$中,对角线$AC$,$BD交于点O$,点$M$,$N分别为OB$,$OC$的中点,求$\cos \angle OMN$的值。

答案： 解:
∵在正方形ABCD中,对角线AC,BD交于点O,
∴∠OBC = 45°.
∵点M,N分别为OB,OC的中点,
∴MN//BC.
∴∠OMN = ∠OBC = 45°.
∴$\cos\angle OMN = \cos45° = \frac{\sqrt{2}}{2}$.

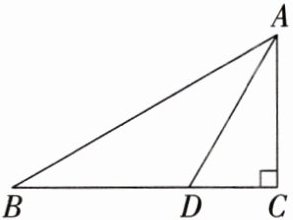
20. 如图,在$\triangle ABC$中,$\angle C = 90^{\circ}$,$\angle B = 30^{\circ}$,$AD是\angle BAC$的平分线,与$BC相交于点D$,且$AB = 4\sqrt{3}$,求$AD$的长。

答案： 解:在Rt△ABC中,
∵∠B = 30°,
∴AC = $\frac{1}{2}$AB = $\frac{1}{2}×4\sqrt{3}$ = 2$\sqrt{3}$.
∵AD平分∠BAC,
∴∠CAD = 30°.在Rt△ACD中,AD = $\frac{AC}{\cos30°} = \frac{2\sqrt{3}}{\frac{\sqrt{3}}{2}} = 4$.

21. 如图,在$\triangle ABC$中,$\angle C = 150^{\circ}$,$AC = 4$,$\tan B = \dfrac{1}{8}$。
(1)求$BC$的长；
(2)利用此图形求$\tan 15^{\circ}$的值。

答案：
解:
(1)如图,过A作AD⊥BC,交BC的延长线于点D,
∵∠ACB = 150°,
∴∠ACD = 30°.在Rt△ADC中,
∵AC = 4,
∴AD = AC·$\sin30° = \frac{1}{2}$AC = 2,CD = AC·$\cos30° = 4×\frac{\sqrt{3}}{2} = 2\sqrt{3}$.在Rt△ABD中,$\tan B = \frac{AD}{BD} = \frac{2}{BD} = \frac{1}{8}$,
∴BD = 16,
∴BC = BD - CD = 16 - 2$\sqrt{3}$.
(2)如图,在BC边上取一点M,使得CM = AC,连接AM,
∵∠ACB = 150°,
∴∠AMC = ∠MAC = 15°,
∴$\tan15° = \tan\angle AMD = \frac{AD}{MD} = \frac{2}{4 + 2\sqrt{3}} = \frac{1}{2 + \sqrt{3}}$ = 2 - $\sqrt{3}$.