第8页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
10. 如图,数轴上的$A$,$B$,$C三点所表示的数分别为a$,$b$,$c$,其中点$A$,$B之间的距离等于点B$,$C$之间的距离。如果$|a|>|c|>|b|$,那么该数轴的原点$O$的位置应该在(
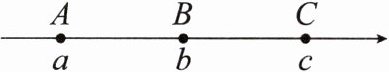
A.点$A$的左边
B.点$A与点B$之间
C.点$B与点C$之间,且靠近点$B$
D.点$C$的右边
C
)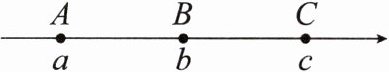
A.点$A$的左边
B.点$A与点B$之间
C.点$B与点C$之间,且靠近点$B$
D.点$C$的右边
答案:
C
11. 若$|a|+|b|= 5$,$a = -1$,则$b= $
$\pm4$
。
答案:
$\pm4$(如果以填空题形式,直接填$\pm4$)
12.(阅读理解题)阅读理解:$|5 - 2|$表示5与2之差的绝对值,$|5 - 2|$也可以利用数轴理解为数轴上5与2这两个数所对应的两点之间的距离,如图所示。
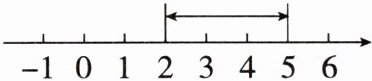
问题解决:(1)$|-5 - 2|= $______
(2)求使$|x - (-5)|= 7$成立的所有整数。

问题解决:(1)$|-5 - 2|= $______
7
,这个算式利用数轴可理解为______数轴上$-5$与$2$这两个数所对应的两点之间的距离
;(2)求使$|x - (-5)|= 7$成立的所有整数。
答案:
(1)
$7$;数轴上$-5$与$2$这两个数所对应的两点之间的距离。
(2)
因为$\vert x - (-5)\vert = 7$,即$\vert x + 5\vert = 7$。
则$x + 5 = 7$或$x + 5 = -7$。
当$x + 5 = 7$时,$x = 7 - 5 = 2$;
当$x + 5 = -7$时,$x = -7 - 5 = -12$。
所以使$\vert x - (-5)\vert = 7$成立的所有整数为$2$和$-12$。
(1)
$7$;数轴上$-5$与$2$这两个数所对应的两点之间的距离。
(2)
因为$\vert x - (-5)\vert = 7$,即$\vert x + 5\vert = 7$。
则$x + 5 = 7$或$x + 5 = -7$。
当$x + 5 = 7$时,$x = 7 - 5 = 2$;
当$x + 5 = -7$时,$x = -7 - 5 = -12$。
所以使$\vert x - (-5)\vert = 7$成立的所有整数为$2$和$-12$。
查看更多完整答案,请扫码查看


