《2025年人教金学典同步解析与测评七年级数学上册人教版重庆专版》

1. 若 $ a^{2}+|b + 1| = 0 $,则 $ (a + b)^{2025} $ 的值为(A)
A.$-1$
B.$0$
C.$1$
D.$2$

答案： A

2. 若 $ m^{2}+2m - 1 = 0 $,则 $ 2m^{2}+4m - 3 $ 的值是(A)
A.$-1$
B.$-5$
C.$5$
D.$-3$

答案： A

3. 若 $ a$,$b $ 非零且互为相反数,$c$,$d $ 互为倒数,$m $ 的绝对值为 $ 2 $,则 $ m^{2}-cd+\frac{a + b}{m} $ 的值为(C)
A.$-4$
B.$0$
C.$3$
D.$5$

答案： C

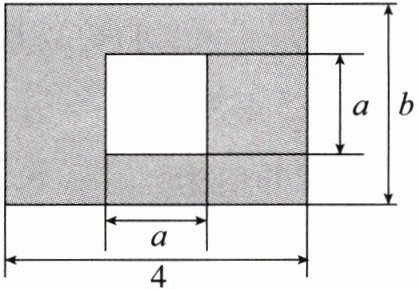
4. 某市有一块长为 $ 4\ m $、宽为 $ b\ m $ 的长方形地块,如图所示(单位：$m$)。规划部门计划将阴影部分绿化,中间正方形空地将修建一座雕像。用含 $ a$,$b $ 的式子表示绿化的面积是$4b - a^2$$m^{2}$,若 $ a = 2$,$b = 3 $,则绿化面积是$8$$m^{2}$。

答案： $4b - a^2$ ，$8$。

5. 甲、乙两景点是某平台国庆期间某热门景点前两名,已知甲景点门票每张 $ 100 $ 元,乙景点门票每张 $ 45 $ 元,在某个时间段内,共售出 $ a $ 张甲景点门票和 $ b $ 张乙景点门票。
(1)在该时间段内,该平台这两种门票共售出多少元？
(2)当 $ a = 30000$,$b = 8000 $ 时,该平台这两种门票共售出多少元？(用科学记数法表示)

答案：
(1) 甲景点门票收入为 $100a$ 元，乙景点门票收入为 $45b$ 元，两种门票共售出$(100a + 45b)$元。
(2) 当 $a = 30000$，$b = 8000$ 时，
$\begin{aligned}100a + 45b &= 100×30000 + 45×8000 \\&= 3000000 + 360000 \\&= 3360000 \\&= 3.36×10^6\end{aligned}$
该平台这两种门票共售出 $3.36×10^6$ 元。

6. 如图所示,按程序计算,若输入 $ x $ 的值为 $ 3 $,则输出的值为-3。

答案： -3

7. 如图,两摞规格相同的数学课本整齐地叠放在课桌上,请根据示意图中的数据信息,解答下列问题：
(1)每本数学课本的高度为0.5$cm$,课桌的高度为85$cm$；
(2)当数学课本为 $ x $ 本时,同样叠放在桌面上的一摞数学课本高出地面的距离为$85 + 0.5x$$cm$(用含 $ x $ 的代数式表示)；
(3)桌面上有 $ 55 $ 本数学课本,整齐叠放成一摞,若有 $ 18 $ 名同学各从中取走 $ 1 $ 本,求余下的数学课本高出地面的距离。
103.5

答案：
(1) 设每本数学课本的高度为 $ h $ cm，课桌的高度为 $ k $ cm。由图可知，3本课本叠放时总高度为86.5cm，6本课本叠放时总高度为88cm，可列方程组：
$\begin{cases}k + 3h = 86.5 \\k + 6h = 88\end{cases}$
用第二个方程减去第一个方程：$ 3h = 1.5 $，解得 $ h = 0.5 $。将 $ h = 0.5 $ 代入第一个方程：$ k + 3×0.5 = 86.5 $，解得 $ k = 85 $。故每本数学课本的高度为 $ 0.5 $ cm，课桌的高度为 $ 85 $ cm。
(2) 当有 $ x $ 本数学课本时，高出地面的距离为课桌高度加上 $ x $ 本课本的高度，即 $ 85 + 0.5x $ cm。
(3) 原有55本，取走18本后，剩余 $ 55 - 18 = 37 $ 本。代入
(2)中的代数式：$ 85 + 0.5×37 = 85 + 18.5 = 103.5 $ cm。
(1) 0.5；85
(2) $ 85 + 0.5x $
(3) 103.5