第71页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
1. 下列四个立体图形中,是三棱柱的为(

C
)
答案:
C
2. 某立体图形的展开图如图所示,该立体图形是(

A.长方体
B.正方体
C.圆锥
D.圆柱
C
)
A.长方体
B.正方体
C.圆锥
D.圆柱
答案:
C
3. 如图,该正方体的展开图为(


B
)

答案:
B
4. 一正方体的展开图如图所示,分别填上数字 1,2,3,4,5,6,使得折叠成正方体后,相对面上的数字之和相等,则 $ a = $

6
,$ b = $2
,$ c = $4
。
答案:
1. 首先分析正方体展开图相对面的关系:
对于正方体展开图,“$1 - 4$型”(本题属于这种类型),相对面的规律是:同行或同列间隔一个面的两个面是相对面。
在这个展开图中,$1$与$a$是相对面,$3$与$c$是相对面,$5$与$b$是相对面。
2. 然后根据相对面上数字之和相等来计算:
已知数字$1,2,3,4,5,6$,$1 + 2+3 + 4+5 + 6=\frac{6×(1 + 6)}{2}=21$。
因为正方体有$3$组相对面,且相对面数字之和相等,所以每组相对面数字之和为$\frac{21}{3}=7$。
对于$1$与$a$:
由$1 + a=7$,可得$a = 6$。
对于$5$与$b$:
由$5 + b=7$,可得$b = 2$。
对于$3$与$c$:
由$3 + c=7$,可得$c = 4$。
故答案依次为:$6$;$2$;$4$。
对于正方体展开图,“$1 - 4$型”(本题属于这种类型),相对面的规律是:同行或同列间隔一个面的两个面是相对面。
在这个展开图中,$1$与$a$是相对面,$3$与$c$是相对面,$5$与$b$是相对面。
2. 然后根据相对面上数字之和相等来计算:
已知数字$1,2,3,4,5,6$,$1 + 2+3 + 4+5 + 6=\frac{6×(1 + 6)}{2}=21$。
因为正方体有$3$组相对面,且相对面数字之和相等,所以每组相对面数字之和为$\frac{21}{3}=7$。
对于$1$与$a$:
由$1 + a=7$,可得$a = 6$。
对于$5$与$b$:
由$5 + b=7$,可得$b = 2$。
对于$3$与$c$:
由$3 + c=7$,可得$c = 4$。
故答案依次为:$6$;$2$;$4$。
5. 由若干个完全相同的小正方体组成的一个立体图形如图所示,请在方格纸中用实线画出这个立体图形分别从前面、左面、上面观察得到的平面图形。




答案:

6. (开放题)一个立体图形从前面、左面、上面观察,得到的平面图形完全相同,该立体图形可以是
正方体
。(写出一个即可)
答案:
正方体
7. 用若干个大小相同的小正方体搭一个立体图形,使得从该立体图形的前面、上面观察,所得到的平面图形如图所示,搭成这样一个立体图形,最少需要多少个小正方体?最多需要多少个小正方体?在上述两种情况下,请分别画出从左面观察对应的立体图形,所能得到的平面图形。


答案:
最少需要8个小正方体,最多需要11个小正方体。
最少时从左面看的平面图形:
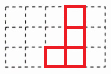
最多时从左面看的平面图形:
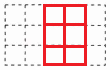
最少需要8个小正方体,最多需要11个小正方体。
最少时从左面看的平面图形:

最多时从左面看的平面图形:

查看更多完整答案,请扫码查看


